- ...
ギルバート1.1
- 肖像画はすべてWikipediaから
転載している。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
2種類1.2
- 琥珀、エボナイト、ガラスなど
多数の物質に生じる電気が2種類だけであるという理解は、電気現象に
理解のために重要な発展であった。素粒子を構成するクォークでは
3種類の「電荷」に相当するものが存在することに対比できるだろう。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
同種のもの同士は反発して1.3
- 引力の場合, 静電誘導現象により
プラス電気もマイナス電気も電気を帯びていない物質を引きつける。
従って引力で電荷の正負を判定することは困難である。
この静電誘導の理解は20世紀になって物質の電子論が
発展して始めて理解できた。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 」1.4
- 電池の原理の簡単な説明:
希硫酸という溶液には水素イオン(+イオン)と硫酸イオン(−イオン)が
存在する。この中に亜鉛と銅を入れると、銅に比べてイオン化傾向の大きい
亜鉛は、希硫酸の中に溶け出す。亜鉛は溶け出るとき、電子を二つ残して、
亜鉛イオン(+イオン)になる。亜鉛イオンに追いやられた水素イオンは、
銅の方に寄っていって、銅のところで電子を一個もらって、水素分子に
なって出ていく。(2(H++e-) → H2)こうして、亜鉛側から銅側に電子の
流れができる、すなわち電気が流れる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
なった1.5
- 電場と磁場を統一した電磁場(電磁気力)の概念の芽生え
である。現在自然界には4つの基本的な力、重力、弱い力、電磁気力、
強い力の存在が知られている。その中で弱い力と電磁気力は同じ起源を
持つ力であることが示されている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
正の電荷を持った粒子が流れているように見える場合がある1.6
-
ホール効果の実験によって明らかにされた。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ここでは、フォノンによる散乱に線形性5.1
-
例えば、フォノンの数が増えれば、比例して電子は強く散乱される。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
オームの法則に線形性5.2
- 電流と電圧が比例する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
考える。この回路の中の2つの節点を考えて、その回路の端子対(2端子)5.3
- portと呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
供給することができる。以下の鳳5.4
- 「ほう」と読む。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...であるとしよう5.5
-
電圧源を短絡するのは、電圧源には電流が流れることによる電位差が生じないことに対応
する。一方、電流源を開放するのは枝の両端の電位差に関係なく一定の電流が流
れることに対応する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
各瞬間毎にオームの法則が成り立つから6.1
-
抵抗はダイナミカルシステムにおける状態を記憶する素子にはならない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
となる6.2
- 現在の時刻
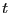 ではない時刻
ではない時刻
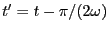 での電圧
での電圧
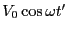 によって、現在の電流が決定されてい
る。
によって、現在の電流が決定されてい
る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
となる6.3
- 現在の時刻
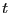 ではない時刻
ではない時刻
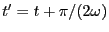 での電圧
での電圧
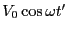 によって、現在の電流が決定されている。
によって、現在の電流が決定されている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
であることが分る6.4
- 抵抗の場合
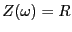 である。
である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...chap:dc_circuit章では、直流回路網6.5
-
抵抗と直流電圧源、直流電流源のみからなる回路網
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...fig:system参照。このようなシステムは工学的に重要である
7.1
-
TVが買った時に応じて視聴できたりできな
かったりすると、そのTVは漸近安定なシステムではないと言うことができる。
このような漸近安定でないシステムは信頼して使うことができない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
が得られる7.2
-
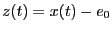 と置くと、微分方程式は
と置くと、微分方程式は
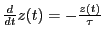 となり、
となり、
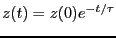 と簡単に解ける。
初期条件を満たすように
と簡単に解ける。
初期条件を満たすように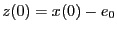 をとれば、上の解が得られる。
をとれば、上の解が得られる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は定数である
7.3
-
時刻
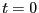 における
における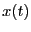 の初期条件を満たすために、
の初期条件を満たすために、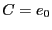 でなければならない。
でなければならない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
の大きさには依存しない。すなわち、システムは漸近安定である7.4
-
一般に
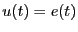 が時間依存する場合は、
が時間依存する場合は、
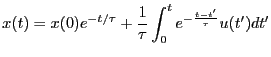 |
|
|
(7.14) |
が得られる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
に対する9.1
- セクション6.2と同様に考えて、実数の入力
関数から複素数の入力関数を作ることができる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
である9.2
-
線形性より
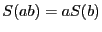 である。ここで
である。ここで
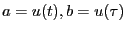 とすると上の
式が得られる
とすると上の
式が得られる
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
このような関数は実は「存在しない」ので9.3
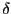 関数は超関数である。
関数は超関数である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
である9.4
-
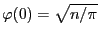 であり、
であり、
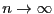 の極限で
の極限で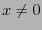 での関数値はゼロに近づく。一方、
での関数値はゼロに近づく。一方、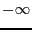 から
から
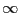 まで積分すると値は1になる。
まで積分すると値は1になる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
とる必要がある9.5
-
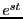 の
の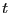 が正なので、半時計回り(正の向き)に積分を行う。
が正なので、半時計回り(正の向き)に積分を行う。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...になり9.6
-
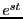 の
の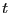 が負なので、時計回り(負の向き)に積分を行う。
が負なので、時計回り(負の向き)に積分を行う。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
再結合して、消滅する10.1
- 動的に空乏層が消失していると見なすこともで
きる
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
加された電圧を打ち消すように働くため、逆方向には電流が流れにくくなる10.2
-
実際の素子では、真性半導体に由来する少数キャリアのために
逆バイアス状態でもごくわずかに逆方向電流が流れる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
から電子がベースに入ってくる10.3
- ダイオードの場合と同様に動的にエ
ミッタ−ベース間の空乏層が消失していて、ベースに電子が入ってくると考えて
も良い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ると言える10.4
- このようなエミッタから注入された電子がベースをすり抜
けることができるように、エミッタの電子密度はベースの正孔密度の100倍程度
に調整されている。また、コレクタの電子密度はベースの正孔密度のさらに100
分の1程度にされ、ベース−コレクタ間の空乏層が大きくなるようになってい
る。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
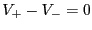 10.5
10.5
-
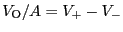 であり、Aが無限大なので
であり、Aが無限大なので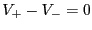 である。大きいけれど、有限のA
の場合には
である。大きいけれど、有限のA
の場合には
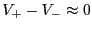 となる。
となる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...が生じる11.1
-
ここでは磁化の発生する機構は議論しない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
始める11.2
- 重力下のコマの運動とよく似ている。コマの運動は解析
力学の講義で議論するだろう。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...となりラーモア周波数と呼ばれる
11.3
-
ローモア周波数はしばしば回転の向きを含めて、
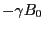 と
提議されることがある。しかしながら、ここでは時計回り、あるいは反時計回り
という言葉を使って、回転の向きを表わし、常に
と
提議されることがある。しかしながら、ここでは時計回り、あるいは反時計回り
という言葉を使って、回転の向きを表わし、常に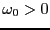 とする。
とする。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
水素や炭素のラーモア周波数はそれぞれ42.59 MHz/T、10.71 MHz/Tである11.4
-
1 Tの磁束密度に対応した磁場内でのラーモア周波数がそれぞれ、
れ42.59 MHz、10.71 MHzという意味である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...があるとしよう11.5
-
このようなラーモア周波数の分布は様々な理由で起こり得る。例えば、
静磁場の不均一性などである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
が測定できると仮定しよう11.6
-
コイルに発生する信号は誘導起電力に依る。従って、
軸がx軸に平行な円筒形のコイルに発せする信号は
に比例する。ただし、
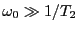 なので
なので
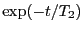 の時間微分に起因する信号は無視している。
の時間微分に起因する信号は無視している。
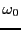 は分かっているので、時間原点をずらすことによって、
x軸方向の信号
は分かっているので、時間原点をずらすことによって、
x軸方向の信号
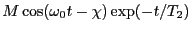 を
得ることができる。
を
得ることができる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
実際に数値計算を行なう場合、以下の物理定数12.1
- この講義では使うことはないが、
炭素の磁気回転比:
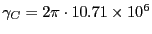 s
s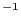 T
は記憶しておくべきである。
T
は記憶しておくべきである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
12.2
- 約2 kHzである。建物内では鉄筋コンクリートや周囲の磁性体(主と
して鉄)による磁気シールドのためか、多少小さくなる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.