



: ラプラス変換の応用例
: ラプラス変換
: ラプラス変換
目次
デルタ関数のラプラス変換について考察する。デルタ関数とは、
となる関数のことである。また、以下の性質もある。
このような関数は実は「存在しない」ので9.3、
という極限で表現することにしよう。
よく使われる関数列は
である9.4。ただし、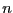 は自然数である。また、単位階段関数(ヘビサイト関数)
は自然数である。また、単位階段関数(ヘビサイト関数)
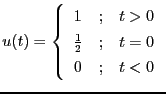 |
|
|
(9.9) |
を使って、
と表すこともできる。
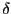 関数のラプラス変換が1になることは以下のように考えて理解する。
関数のラプラス変換が1になることは以下のように考えて理解する。
次にデルタ関数の微分のラプラス変換を考える。ラプラス変換を行なう際の積分
範囲を
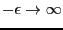 と拡張すれば、部分積分の公式より
と拡張すれば、部分積分の公式より
が成り立つ。ここで
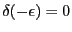 であ
るし、
であ
るし、
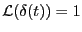 だから、
だから、
と結論づけることにする。同様に、
である。
Administrator
平成25年1月3日
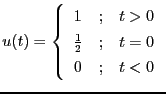
![]() 関数のラプラス変換が1になることは以下のように考えて理解する。
関数のラプラス変換が1になることは以下のように考えて理解する。
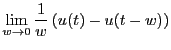 から
の考察
から
の考察
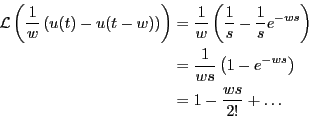
![]() と拡張すれば、部分積分の公式より
と拡張すれば、部分積分の公式より