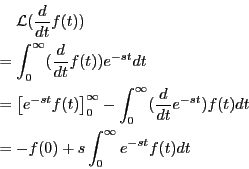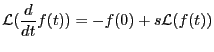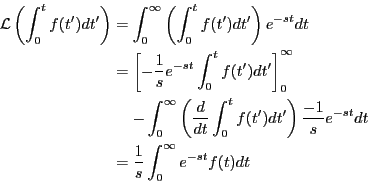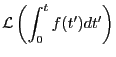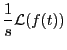: デルタ()関数のラプラス変換
: ラプラス変換
: ラプラス変換
目次
ある時間の関数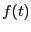 が与えられているとき、
が与えられているとき、
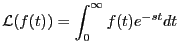 |
|
|
(9.4) |
を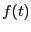 のラプラス変換と言う。
次に示すようにラプラス変換は線形である。
のラプラス変換と言う。
次に示すようにラプラス変換は線形である。
また、
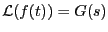 のとき
のとき
となり、相似則と言う。
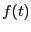 の時間微分をラプラス変換すると、
の時間微分をラプラス変換すると、
もしも、
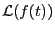 が存在するならば、
が存在するならば、
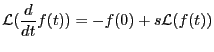 |
|
|
(9.7) |
となる。一方、
すなわち、
である。
よく使われる関数のラプラス変換を
表 9.1にまとめる。




: デルタ()関数のラプラス変換
: ラプラス変換
: ラプラス変換
目次
Administrator
平成25年1月3日
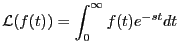
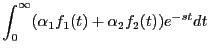
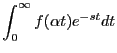
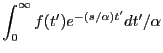
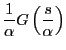
![]() の時間微分をラプラス変換すると、
の時間微分をラプラス変換すると、