



: たたみ込み(コンボリュージョン)と合成法則
: ラプラス変換
: デルタ()関数のラプラス変換
目次
起電力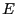 の電池、スイッチ、コイル、抵抗を直列に接続した回路を考え、
時刻
の電池、スイッチ、コイル、抵抗を直列に接続した回路を考え、
時刻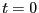 でスイッチをオンにした。過渡応答をラプラス変換を用いて
調べる。
でスイッチをオンにした。過渡応答をラプラス変換を用いて
調べる。
回路のダイナミクスを表わす微分方程式は
である。表 9.1を使えるように、
ある特徴的な時間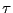 を
導入して時間を無次元化する。すなわち、
を
導入して時間を無次元化する。すなわち、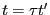 とする。
元に微分方程式は以下のようになる。
とする。
元に微分方程式は以下のようになる。
ラプラス変換を行なうことにより、
が得られる。ただし、題意より時刻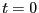 における電流
における電流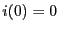 である。
である。
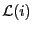 について解くと
について解くと
となる。ここで、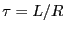 とおくと、
とおくと、
となり、線形性と表 9.1を用いることにより、
が得られる。最後に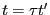 を用いて、
を用いて、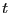 の関数に戻せば、
の関数に戻せば、
が得られる。
Administrator
平成25年1月3日