複素指数関数の入力に対する9.1線形時不変システムの出力は
となる。ここで、証明は次の通りである。出力は
に関する複素関数で、周波数応答関数 と呼ばれる。
上の定理は角振動数![]() の複素指数関数(三角関数)を入力とする線形時不
変システムの出力はやはり複素指数関数(三角関数)になることを
意味している。ただし、入力
の複素指数関数(三角関数)を入力とする線形時不
変システムの出力はやはり複素指数関数(三角関数)になることを
意味している。ただし、入力![]() と出力
と出力![]() の間は周波数応答関数
の間は周波数応答関数
![]() によって
によって
![]() と結ばれている。
と結ばれている。
線形時不変システムのダイナミクスが以下の微分方程式で定義されているとしよ
う。
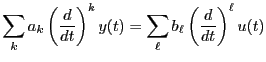 |
(9.1) |
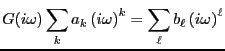 |
(9.2) |
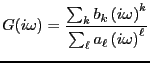 |
(9.3) |