next up previous contents
: 回路 : ダイナミカルシステム : 線形時不変システム   目次

線形時不変システムとしての電気回路

まず、オームの法則について復習しよう。 針金の両端に一定の電圧$V$（単位はV）を与えると 定常電流$I$（単位はA）が得られる。この定常電流は電圧に比例する。 この事実をオームの法則と呼び、 この時の比例定数を抵抗と言う。記号としては$R$を 通常用いる。すなわち、

$\displaystyle V = R I$     (7.9)

となる。抵抗の単位は$V/A$であるが、これをオームと呼び $\Omega$で表す。

ここで$I = u(t)$、$V = y(t)$、 $S(u(t)) = R\, u(t)$と考えれば、 抵抗は電流$I$を入力して電圧$V$を出力する線形時不変システムと 考えることができるのは明らかであろう。

もう少し複雑な例として、電源、抵抗、コンデンサーが 直列につながった回路を考えよう。抵抗の両端の電圧を 出力$y(t)$と考える。一方入力$u(t)$はある時刻に おける電池の電圧$e(t)$である。また、システムの状態$x(t)$を 表すのはコンデンサーの電圧$v(t)$である。

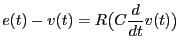$\displaystyle e(t) - v(t) = R \bigl(C\frac{d}{dt} v(t)\bigr)$     (7.10)

である。ここで$RC = \tau$と書くことにすれば、状態方程式は
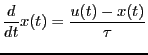$\displaystyle \frac{d}{dt}x(t) = \frac{u(t) - x(t)}{\tau}$     (7.11)

となり、出力方程式は
$\displaystyle y(t) = u(t)-x(t)$     (7.12)

である。電源電圧$u(t)=e(t)$が$t=0$に $0 \rightarrow e_0$に変化する場合を考えよ う。$t\ge 0$において微分方程式を解くと、
$\displaystyle x(t) = (x(0)-e_0)e^{-t/\tau} + C$     (7.13)

が得られる 7.2。 ただし、$C$は定数である 7.3。 $t \rightarrow \infty$の場合を考えると状態$x(t)$は初期状態 $x(0)$ に依存しないことが分る。言い換えると最初コンデンサーに蓄えられていた電荷 の大きさには依存しない。すなわち、システムは漸近安定である 7.4。

電源（入力）の直列接続は新しい一つの電源と考えることができるから、 入力と出力の線形性は 明らかである。一方、時不変性は物理法則における時間原点の任意性から明らか である。


Administrator 平成25年1月3日