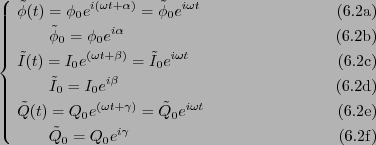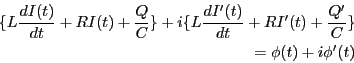複素インピーダンス

セクション6.1で示したように回路にコイルやキャパシター がある場合は微分方程式を解けば、回路の振る舞いを知ることができる。しかし ながら、微分方程式を解くのは大変なので以下のような考えに従って複素 インピーダンスを導入すると便利である。

交流起電力が

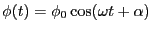$$\phi(t) = \phi_0 \cos ( \omega t + \alpha )$$ (6.1)

と与えられている場合を考える。この起電力によって生じる電流や電荷も同じ振 動数で振動するであろう。従って、

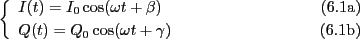
となる。位相は異なる可能性があることに注意。 そして、次のような複素数の関数を作る。

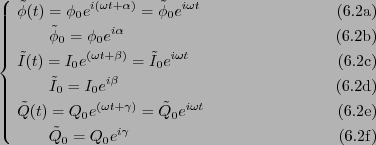
これらの関数の実数部は物理的に意味がある式に一致する。これらの関数が解く べき微分方程式を満たしてると仮定しよう。例えば、

$$\begin{eqnarray*} L\frac{d\tilde{I}(t)}{dt} + R \tilde{I}(t) + \frac{\tilde{Q}}{C} = \tilde{\phi}(t) \end{eqnarray*}$$

などである。ここで、実数部と虚数部に分けると、

$$\begin{eqnarray*} \{L\frac{dI(t)}{dt} + R I(t) + \frac{Q}{C}\} +i \{L\frac{dI'(t)}{dt} + R I'(t) + \frac{Q'}{C}\} \\ = \phi(t) + i \phi'(t) \end{eqnarray*}$$

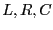となる。$L,R,C$はすべて実数だから$\{\,\}$の中は実数であり、右辺と左辺で それぞれの実数部と虚数部が等しくないといけない。従って、まず複素数の関数 を用いて問題を解いた後、その実数部分のみを取り出せば物理的に意味のある解 を得ることができる。