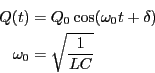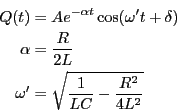: 複素インピーダンス
: 微分方程式と基本回路素子
: 実効値
目次
電気振動
下図の回路でキャパシター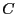 に電荷
に電荷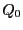 を蓄えた後、スイッチS
を閉じる。この時、回路に流れる電流を
を蓄えた後、スイッチS
を閉じる。この時、回路に流れる電流を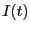 とすると、
とすると、
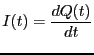 である。ここで
である。ここで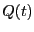 は
各瞬間においてキャパシターに蓄えられている電荷である。
は
各瞬間においてキャパシターに蓄えられている電荷である。
回路を一周する時の起電力の総和は
である。
特に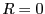 の場合は
の場合は
となるから、電荷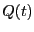 は
は
の単振動を行う。また、抵抗がゼロでない場合の解は
であり、減衰振動を行う。ここで、液体中の単振り子と比較すると
コイルが「慣性」の、キャパシターが「復元力」の役を
担っていることが分かる。抵抗はもちろん「抵抗」の役である。
Administrator
平成25年1月3日
![\includegraphics[width=3cm]{fig86.eps}](img326.png)
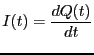 である。ここで
である。ここで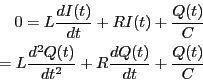
![]() の場合は
の場合は