



: 問題
: NMRの原理
: スピンエコー
目次
NMR装置と信号検出
NMR装置の概略を図 11.7に示した。
図 11.7:
NMR装置の概略。発振器(Oscillator)とパルス発生器
(Pulse Generator)によって
高周波パルスが生成される。高周波パルスは同調回路に導入され、コイルに
振動磁場が生成され、試験管(test tube)内の試料の磁化を制御する。
試料の磁化の運動はコイルに誘導起電力を誘起する。
この信号は増幅され、検出される。LPFとADCはそれぞれローパスフィルターと
アナログ-ディジタル変換器を意味している。方向性結合器(Directional
Coupler)が図で示すように、
信号の流れを制御する。混合機(mixer)は二つの入力の掛算を行なう。
|
|
高周波はパルス発生器の出力に
応じて成形され、高周波パルスになる。これらの高周波パルスは、増幅され
同調回路に導入される。そして、振動磁場(既に議論したように回転磁場と
等価)がコイルに生成され、試験管内の試料の磁化を制御する。試料の
磁化によって同調回路に誘導機電力が誘起される。この信号は増幅された後に
検出される。同調回路を用いるのは、強い振動磁場と大きな信号を得るため
である。
信号の検出方法について議論しよう。もしも緩和が存在しないのならば、
xy面内の
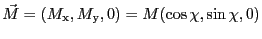 は一定である。しかしながら、横緩和のために、
は一定である。しかしながら、横緩和のために、
のように減少する。ただし、 を仮定し、縦緩和は
無視している。
を仮定し、縦緩和は
無視している。 はNMRにおいては珍しくないことに注意。
実験室系で磁化をみると、
はNMRにおいては珍しくないことに注意。
実験室系で磁化をみると、
となる。 はラーモア周波数で、回転は時計回りである。
実験室系における磁化のx成分
はラーモア周波数で、回転は時計回りである。
実験室系における磁化のx成分
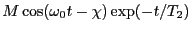 が測定できると仮定しよう11.6 。
この信号のことを
Free Induction Decay (= FID) 信号と呼ぶ。
が測定できると仮定しよう11.6 。
この信号のことを
Free Induction Decay (= FID) 信号と呼ぶ。
このFID信号に
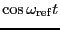 を掛算すると、
を掛算すると、
が得られる。ただし、
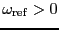 で、
で、
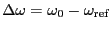 とする。
高い周波数(
とする。
高い周波数(
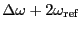 )の成分を落とすと
)の成分を落とすと
が得られる。この操作はカットオフ周波数が
 より
十分低いローパスフィルターに信号を通すことによって
行なわれる。同様に、FID信号に
より
十分低いローパスフィルターに信号を通すことによって
行なわれる。同様に、FID信号に
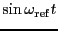 を掛算することによって、
を掛算することによって、
が得られる。周波数の大きさの程度は
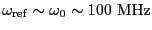 ,
,
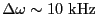 、 そして
、 そして
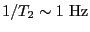 となっていることに注意。次に複素数の関数
となっていることに注意。次に複素数の関数
を定義しよう。ただし、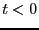 では、
では、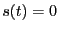 とする。フーリエ変換によって
とする。フーリエ変換によって
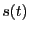 を周波数空間の関数(スペクトル)に変換すると、
を周波数空間の関数(スペクトル)に変換すると、
となる。
図 11.8:
吸収および分散スペクトル。
吸収曲線の極大を与える周波数から
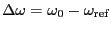 がわかり、
がわかり、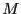 と
と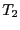 は極大の高さと半値全幅(FWHH)から求まる。
は極大の高さと半値全幅(FWHH)から求まる。
|
|
もしも、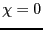 ならば,
ならば, 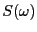 の実数部分は中心を
の実数部分は中心を 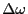 とする吸収(ローレンツ)曲線
とする吸収(ローレンツ)曲線
になる。
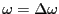 における高さが
における高さが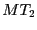 を与え、
を与え、
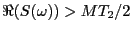 となる領域(半値全幅、FWHHと呼ぶ)が
となる領域(半値全幅、FWHHと呼ぶ)が
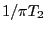 を与える。
このようにして、
を与える。
このようにして、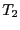 と
と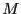 をスペクトルから求めることができる。
一方、
をスペクトルから求めることができる。
一方、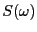 の虚数部分は分散(ローレンツ)曲線
の虚数部分は分散(ローレンツ)曲線
を与える。
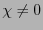 の場合には、スペクトルの実数部分、虚数部分は吸収曲線と分散
曲線の線形結合になる。
の場合には、スペクトルの実数部分、虚数部分は吸収曲線と分散
曲線の線形結合になる。
Administrator
平成25年1月3日
![\includegraphics[width=8.5cm]{ns_v_7.eps}](img819.png)
![\includegraphics[width=8.5cm]{ns_v_7.eps}](img819.png)
![]() は一定である。しかしながら、横緩和のために、
は一定である。しかしながら、横緩和のために、
![]() を掛算すると、
を掛算すると、
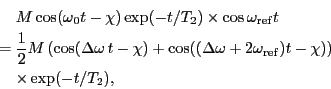
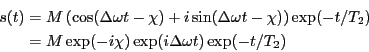
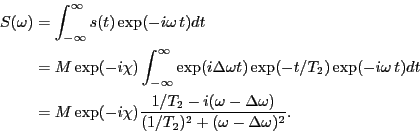
![]() ならば,
ならば, ![]() の実数部分は中心を
の実数部分は中心を ![]() とする吸収(ローレンツ)曲線
とする吸収(ローレンツ)曲線