



: 問題
: 基本法則II
: 重ね合わせの原理
目次
多数の直流電圧源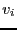 、直流電流源
、直流電流源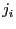 、それに抵抗
、それに抵抗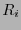 で作られた回路を
考える。この回路の中の2つの節点を考えて、その回路の端子対(2端子)
5.3としよう。この端子対を通じて、回路にパワーを
供給することができる。以下の鳳5.4-
テブナンの定理を用いると、回路をブラック
ボックス化することができ、解析を行う上で有用である。
で作られた回路を
考える。この回路の中の2つの節点を考えて、その回路の端子対(2端子)
5.3としよう。この端子対を通じて、回路にパワーを
供給することができる。以下の鳳5.4-
テブナンの定理を用いると、回路をブラック
ボックス化することができ、解析を行う上で有用である。
回路に含まれるすべての電圧源を短絡し、すべての電流源を開放した時の回路の
合成抵抗が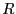 であるとしよう5.5。次に、何も接続せず端子対に現れる電圧は
であるとしよう5.5。次に、何も接続せず端子対に現れる電圧は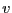 で
あった。この端子対に抵抗
で
あった。この端子対に抵抗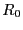 を接続すると電流
を接続すると電流
が流れる。
図 5.6:
鳳−テブナンの定理。どのように複雑な回路でも
電圧源とそれに直列に接続された抵抗と見なすことができる。
|
|
証明は電子回路の線形性を用いて行う。端子対に抵抗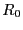 を繋いだ回路は、
図5.7に示すように、
を繋いだ回路は、
図5.7に示すように、
- 電圧源は短絡し、電流源は開放して抵抗のみのネットワークによる合成抵
抗と外部に電圧
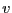 をもつ電圧源と抵抗
をもつ電圧源と抵抗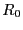 の直列接続回路(下段左側)
の直列接続回路(下段左側)
- 端子対に現れる電圧をキャンセルするように電圧源を接続した回路(下段右側)
図 5.7:
鳳−テブナンの定理の証明。上段の回路は下段の二つの回路の重ね合わせと
考えることができる。下段右側の回路に電流は流れないことに注意。
|
|
の二つの回路の重ね合わせと考えることができる。下段右側の回路の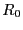 には
電流が流れない。従って、回路の線形性により下阪左側の
には
電流が流れない。従って、回路の線形性により下阪左側の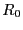 に流れる電流は
上段の回路の
に流れる電流は
上段の回路の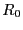 に流れる電流と同じである。
に流れる電流と同じである。
同様に電流源と並列に接続された抵抗によって、等価回路を作ることもできる。
回路に含まれるすべての電圧源を短絡し、すべての電流源を開放した時の回路の
合成抵抗が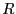 であるとしよう。次に、端子間を短絡した時に流れる電流が
であるとしよう。次に、端子間を短絡した時に流れる電流が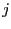 で
あった。この端子対に抵抗
で
あった。この端子対に抵抗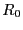 を接続すると、電圧
を接続すると、電圧
が生じる。
図5.8を証明すれば十分であろう。左側の回路の抵抗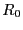 に
流れる電流
に
流れる電流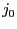 は
は
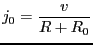 である。一方右側の回路で
である。一方右側の回路で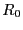 に流れ
る電流は、
に流れ
る電流は、
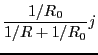 である。ここで、
である。ここで、
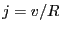 ととれば、
ととれば、
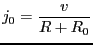 となり、左側の回
路で抵抗
となり、左側の回
路で抵抗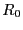 に流れる電流と同じ電流が右側の回路の抵抗
に流れる電流と同じ電流が右側の回路の抵抗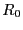 に流れるように
することができる。
に流れるように
することができる。
図 5.8:
任意の回路は電流源とそれに並列に接続された抵抗と等価である。
|
|
Administrator
平成25年1月3日
であるとしよう5.5。次に、何も接続せず端子対に現れる電圧は
で あった。この端子対に抵抗
を接続すると電流
![]() を繋いだ回路は、
図5.7に示すように、
を繋いだ回路は、
図5.7に示すように、
であるとしよう。次に、端子間を短絡した時に流れる電流が
で あった。この端子対に抵抗
を接続すると、電圧
![]() に
流れる電流
に
流れる電流![]() は
は
![]() である。一方右側の回路で
である。一方右側の回路で![]() に流れ
る電流は、
に流れ
る電流は、
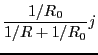 である。ここで、
である。ここで、
![]() ととれば、
ととれば、
![]() となり、左側の回
路で抵抗
となり、左側の回
路で抵抗![]() に流れる電流と同じ電流が右側の回路の抵抗
に流れる電流と同じ電流が右側の回路の抵抗![]() に流れるように
することができる。
に流れるように
することができる。