: 線形時不変システム
: ダイナミカルシステム
: ダイナミクス
目次
時刻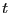 における状態を
における状態を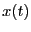 とする。
とする。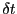 だけ未来の状態
だけ未来の状態
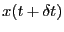 は状態
は状態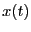 とダイナミクスを表す時刻
とダイナミクスを表す時刻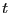 における
ある関数
における
ある関数
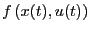 によって、
によって、
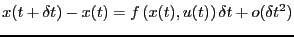 |
|
|
(7.1) |
と表すことができる。ここで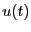 はダイナミクスを規定する
外部変数であり、
はダイナミクスを規定する
外部変数であり、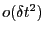 は
は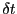 に関する2次以上の微少量であ
る。
に関する2次以上の微少量であ
る。
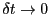 の極限を考えると、
の極限を考えると、
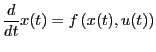 |
|
|
(7.2) |
となり、これを状態方程式と呼ぶ。ここで、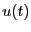 は入力と考えることが
できる。出力
は入力と考えることが
できる。出力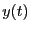 は状態
は状態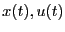 の関数として、
の関数として、
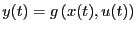 |
|
|
(7.3) |
と表すことができて、出力方程式と呼ぶ。
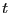 が十分大きくなったとき、初期状態によらず
が十分大きくなったとき、初期状態によらず
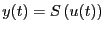 |
|
|
(7.4) |
のように入力と出力が写像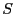 で結ばれるようなシステムを漸近安定なシステム
と呼ぶ。別の言い方をすれば、
初期状態を忘れることができるダイナミカルシステムである。
図 7.1参照。このようなシステムは工学的に重要である
7.1。
で結ばれるようなシステムを漸近安定なシステム
と呼ぶ。別の言い方をすれば、
初期状態を忘れることができるダイナミカルシステムである。
図 7.1参照。このようなシステムは工学的に重要である
7.1。
図 7.1:
漸近安定なダイナミカルシステムの入出力関係
|
|
写像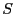 は因果律を満たす必要がある。すなわち、現在の出力は過去の入力のみ
に依存し、未来の入力には依存しないことである。時刻
は因果律を満たす必要がある。すなわち、現在の出力は過去の入力のみ
に依存し、未来の入力には依存しないことである。時刻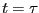 以前の
入力のみを取り出す演算子
以前の
入力のみを取り出す演算子
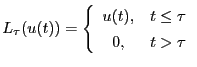 |
|
|
(7.5) |
を導入して数式で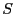 が因果律を満たすことを表すと、
が因果律を満たすことを表すと、
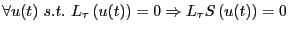 |
|
|
(7.6) |
となる。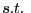 はsuch thatの略である。上の式は
はsuch thatの略である。上の式は
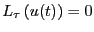 を満たすようなすべての
を満たすようなすべての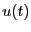 に対して
に対して
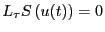 となることを意味している。
となることを意味している。
Administrator
平成25年1月3日
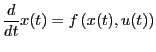
![]() が十分大きくなったとき、初期状態によらず
が十分大きくなったとき、初期状態によらず
![]() は因果律を満たす必要がある。すなわち、現在の出力は過去の入力のみ
に依存し、未来の入力には依存しないことである。時刻
は因果律を満たす必要がある。すなわち、現在の出力は過去の入力のみ
に依存し、未来の入力には依存しないことである。時刻![]() 以前の
入力のみを取り出す演算子
以前の
入力のみを取り出す演算子