...は自然数の集合である^1.1

s. t.はsuch thatを省略したものであり、A s. t. B とは、Bを満たすA という意味である。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... と表されることは良く理解していることであろう^1.2

ここでは、数学的な整合性はあまり考えずに、3つの数の組みで 表現されるものをベクトルとする。本当はベクトルの持つべき 性質を考えて、これらの数の組がその条件を満たすと捉えるべきである

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...と表記されているので、注意のこと^1.3

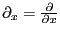$\partial_x = \frac{\partial}{\partial x}$のことである。 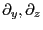$\partial_y, \partial_z$も同様である。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...を対応させると同じ^2.1

導体表面を 越えて電流が流れることはないので、導体表面の近傍では電流も電場も 表面に平行になる。このような境界条件は静電場の場合には存在せず、 全く同じという訳ではない。しかし、これらの違いは導体表面の近傍に 限られる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...)はこの電流による磁気モーメントである^2.2

参考書とは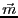$\vec{m}$の 定義が異なっている点に注意。参考書はMKSA単位系を採用しているのに対して、 本講義ではSI単位系を採用している。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... であることによっている^2.3

すべてのベクトル場は渦無し場と渦有り場の和として 表すことができることを思い出すこと。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 満たされるので^2.4

ベクトル演算の公式 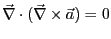$\vec{\nabla}\cdot(\vec{\nabla}\times \vec{a}) = 0$を思い出すこと。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... であるから^2.5

ベクトル演算の公式を思い出すこと

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...を求めることができる^2.6

ポアソン方程式

$$\vec{\nabla}^2 \phi(\vec{r}) = - \rho(\vec{r})$$

の解は

$$\phi(\vec{r}) = \frac{1}{4\pi} \int \frac{\rho(\vec{r})} {\vert\vec{r} - \vec{r} '\vert}dV'$$

で与えられる。ベクトル・ポテンシャルの場合 は各成分毎にポアソン方程式を解けば良い。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... いる^3.1

電磁場の単位体積当たりの運動量は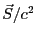$\vec{S}/c^2$によって表される。詳しくは 参照文献[2]を見ること。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... の電流である。^3.2

この式は単位系としてEB対応を採用した場合である。EH対応の場合には

$$\vec{H}(\vec{r}) = \frac{1}{\mu_0}\{ \vec{B}(\vec{r}) - \vec{M}(\vec{r})\}$$

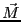である。ここでは$\vec{M}$ の定義が異なっており、

$$\vec{M}({\rm EH}) = \mu_0\vec{M}({\rm EB})$$

である。SI単位系ではEB対応の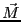$\vec{M}$を用いるのが通常である。 EH対応とEB対応についての詳細は文献 [3] を参考のこと。EB対応を用いて講義を行うので、長岡の教科書と対比する 場合は注意のこと。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.