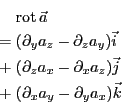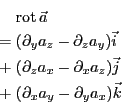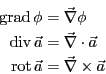: ガウスの定理
: ベクトルに対する微積分
: ベクトルの微分
目次
空間の各点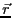 にベクトル関数
にベクトル関数
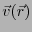 を指定するとき、ベク
トル場
を指定するとき、ベク
トル場
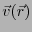 が与えられたと言う。ベクトル場の例としては、流れ場
や電場、磁場がある。ベクトル場に関連する微分演算子としては、
がある。これらはベクトル演算子(ナブラ)
が与えられたと言う。ベクトル場の例としては、流れ場
や電場、磁場がある。ベクトル場に関連する微分演算子としては、
がある。これらはベクトル演算子(ナブラ)
を導入することによって、
と簡便に表すことができる。ここではナブラのベクトル的な
性質を強調するために、 と表記している。
多くの場合
と表記している。
多くの場合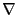 と表記されているので、注意のこと1.3。
と表記されているので、注意のこと1.3。
Administrator
平成25年7月6日