今、微小体積![]() を考察する。具体的なイメージを
掴むために、
を考察する。具体的なイメージを
掴むために、
![]() と考えて流体の流れを
考えよう。ここで、
と考えて流体の流れを
考えよう。ここで、![]() と
と![]() は流体の密度とその速度
である。
は流体の密度とその速度
である。
この微小体積に![]() 方向に沿って流出する流体の量を
考える。図の灰色の面からこの微小体積に流入する
流体の量は
方向に沿って流出する流体の量を
考える。図の灰色の面からこの微小体積に流入する
流体の量は
![]()
である。一方、図の黒色の面から流れ出す流体の量は
![]()
である。よって正味の流出量は
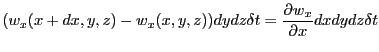
となる。同様に![]() 方向と
方向と![]() 方向にも考察を行い、それらを
合計すると、この微小体積から
方向にも考察を行い、それらを
合計すると、この微小体積から![]() の間に流出する
流体の量は
の間に流出する
流体の量は
次に、空間に閉曲面![]() とこの閉曲面に囲まれている
空間の領域
とこの閉曲面に囲まれている
空間の領域![]() を考察する。
を考察する。![]() を微小体積の集まりと
考えて、
を微小体積の集まりと
考えて、
![]() を
考えよう。
ある一つの微小体積のある面から流出する流体の量は
その同じ面を共通に持つ隣の微小体積に流入する流体の
量と同じである。結局、
を
考えよう。
ある一つの微小体積のある面から流出する流体の量は
その同じ面を共通に持つ隣の微小体積に流入する流体の
量と同じである。結局、![]() 内のすべての
微小体積の表面を通して流入出する流体の
総和は、隣に微小体積を持たない微小体積に流入出する
流体の量、すなわち閉曲面
内のすべての
微小体積の表面を通して流入出する流体の
総和は、隣に微小体積を持たない微小体積に流入出する
流体の量、すなわち閉曲面![]() を通して流入出する
流体の総和
を通して流入出する
流体の総和
![]() になる。
になる。