



: 問題1.4.1
: ベクトルに対する微積分
: ガウスの定理
目次
あるベクトル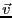 が与えられているとき、
が与えられているとき、
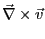 を考える。
これを
を考える。
これを
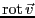 と表記することもある。
と表記することもある。
の式が成り立つ。
ここで、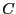 は空間中の閉曲線で、
は空間中の閉曲線で、 は閉曲線
は閉曲線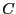 を縁とする
曲面である。閉曲線のある点
を縁とする
曲面である。閉曲線のある点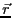 における接線ベクトル
における接線ベクトル
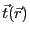 を導入して、
を導入して、
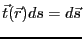 と
書いている。上の式を「ストークスの定理」と言う。
と
書いている。上の式を「ストークスの定理」と言う。
この定理は次のようにして証明される。
図1.9のように微小な長方形PQRSを考える。この長方形は流体の
流れにさらされている。その流速を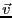 とする。
この長方形に沿って
とする。
この長方形に沿って
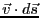 を計算すると、
を計算すると、
となる。
次に閉曲線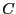 とそれを縁とするような曲面
とそれを縁とするような曲面 を考える。
図 1.10参照。
この曲面を微小面積に分割して
を考える。
図 1.10参照。
この曲面を微小面積に分割して
を求めよう。これは、上の議論を用いて
微小面積のすべての縁について
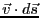 を計算しその総和を求めることに
よっても得られる。しかしながら、
隣り合う微小面積の間でキャンセルする部分があるので、
結局閉曲線
を計算しその総和を求めることに
よっても得られる。しかしながら、
隣り合う微小面積の間でキャンセルする部分があるので、
結局閉曲線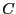 に沿って
に沿って
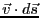 を計算したもの、
すなわち、
を計算したもの、
すなわち、
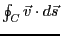 と等しい。
と等しい。
Administrator
平成25年7月6日
![]() とする。
この長方形に沿って
とする。
この長方形に沿って
![]() を計算すると、
を計算すると、
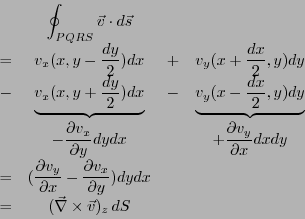
![]() とそれを縁とするような曲面
とそれを縁とするような曲面![]() を考える。
図 1.10参照。
この曲面を微小面積に分割して
を考える。
図 1.10参照。
この曲面を微小面積に分割して