



: ベクトル・ポテンシャル
: ベクトル・ポテンシャル
: 静電ポテンシャルとベクトル・ポテンシャル
目次
静電場
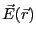 を表す
静電ポテンシャル
を表す
静電ポテンシャル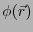 に定数
に定数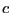 を加えて、新しい静電ポテンシャル
を加えて、新しい静電ポテンシャル
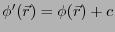 を作っても、元と同じ静電場
を作っても、元と同じ静電場
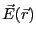 を表すことができる。
を表すことができる。
同様のことがベクトル・ポテンシャル
の場合にもある。すなわち、任意のスカラー関数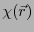 に対して
に対して
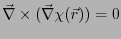 であるから2.5、
であるから2.5、
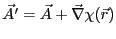 |
|
|
(2.82) |
は、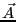 と同じ磁場を作る。このようなベクトル・ポテンシャルの任意性
のおかげで最も便利なベクトル・ポテンシャルを用いることが許される。
と同じ磁場を作る。このようなベクトル・ポテンシャルの任意性
のおかげで最も便利なベクトル・ポテンシャルを用いることが許される。
Administrator
平成25年7月6日
![]() に対して
に対して
![]() であるから2.5、
であるから2.5、