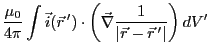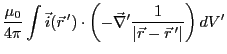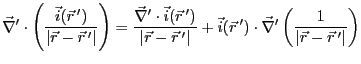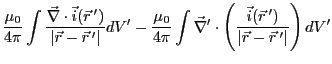: 問題2.7.1
: ベクトル・ポテンシャル
: ベクトル・ポテンシャルの任意性
目次
ベクトル・ポテンシャルが存在することを証明する。電流分布
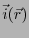 から
から
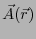 を決めることができれば、証明でき
たことになる。
を決めることができれば、証明でき
たことになる。
式 2.80に
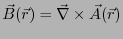 を代入すると、
を代入すると、
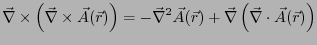 |
|
|
(2.83) |
だから、
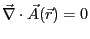 を仮定すると
を仮定すると
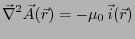 |
|
|
(2.84) |
が得られる。従って、
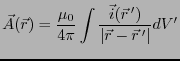 |
|
|
(2.85) |
のように
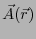 を求めることができる2.6。
を求めることができる2.6。
次にこのようにして求めた
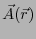 が
が
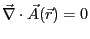 を満たすことを示せば
証明は完了する。定義に従って、
を満たすことを示せば
証明は完了する。定義に従って、
が得られる。ここで
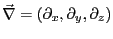 であるのに対して
であるのに対して
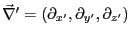 とする。
さらに、
とする。
さらに、
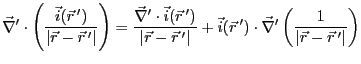 |
|
|
(2.87) |
だから、
となる。定常電流では電荷の保存則より
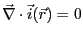 である。一方、
第2項はガウスの定理により表面積分になり、十分大きな体積をとることに
よりその積分はゼロにすることができる。言い換えると,無限に大きな空間に
有限の電流が分布していると無限に大きなエネルギーが必要となり,それは
許されない訳である。以上により、
である。一方、
第2項はガウスの定理により表面積分になり、十分大きな体積をとることに
よりその積分はゼロにすることができる。言い換えると,無限に大きな空間に
有限の電流が分布していると無限に大きなエネルギーが必要となり,それは
許されない訳である。以上により、
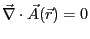 が証明できた。
が証明できた。




: 問題2.7.1
: ベクトル・ポテンシャル
: ベクトル・ポテンシャルの任意性
目次
Administrator
平成25年7月6日
![]() を代入すると、
を代入すると、
![]() が
が
![]() を満たすことを示せば
証明は完了する。定義に従って、
を満たすことを示せば
証明は完了する。定義に従って、