



: ベクトル・ポテンシャルの任意性
: ベクトル・ポテンシャル
: ベクトル・ポテンシャル
目次
静電場
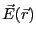 は
は
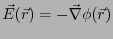 のように
静電ポテンシャル
のように
静電ポテンシャル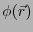 によって表すことが可能である。
このように表すことができるのは、
によって表すことが可能である。
このように表すことができるのは、
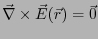 であることによっている2.3。静電場を計算する場合、静電ポテン
シャルをまず求めて、それから電場を計算する方が便利な場合が多い。
であることによっている2.3。静電場を計算する場合、静電ポテン
シャルをまず求めて、それから電場を計算する方が便利な場合が多い。
同様なことが静磁場にもある。ただし、静磁場の基本法則は
である。電流があると渦なしの条件が崩れ、ポテンシャルを定義することが出来
なくなる。そこで、
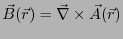 |
|
|
(2.81) |
を考える。このように表すと式 2.79は自動的に
満たされるので2.4、
式 2.80のみを考えれば良いことになる。ただし、この時点では
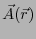 が存在は証明されていない。
が存在は証明されていない。
Administrator
平成25年7月6日