



: 問題2.7.5
: ベクトル・ポテンシャル
: 問題2.7.3
目次
無限に長い半径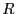 の円筒上に電荷が一様に分布している(面電荷密度は
の円筒上に電荷が一様に分布している(面電荷密度は
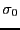 )。円筒を回転させた。円筒の部分での速さを
)。円筒を回転させた。円筒の部分での速さを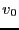 とする。
とする。
- 円筒が回転することによって生じるベクトル・ポテンシャルを求めよ。
- 求めたベクトル・ポテンシャルから磁場を求めよ。
===== 解答 =====
- 半径
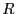 の側面に密度
の側面に密度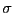 で一様に分布する電荷による電場は
軸から放射状に生じ、軸からの距離が
で一様に分布する電荷による電場は
軸から放射状に生じ、軸からの距離が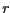 の点における強さは
の点における強さは
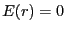
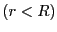 、
、
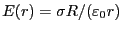
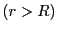 である。
静電ポテンシャルで表すと、
である。
静電ポテンシャルで表すと、
円筒に流れる電流の軸をz軸に取り、
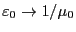 ,
,
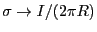 の置き換えを行うと、ベクトル・
ポテンシャル
の置き換えを行うと、ベクトル・
ポテンシャル
が得られる。
-
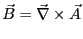 より求まる。
より求まる。
Administrator
平成25年7月6日