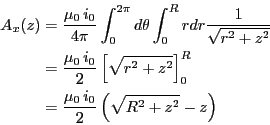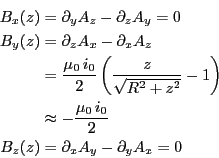: 問題2.7.4
: ベクトル・ポテンシャル
: 問題2.7.2
目次
非常に大きな半径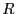 の円盤上に電荷が一様に分布している(面電荷密度は
の円盤上に電荷が一様に分布している(面電荷密度は
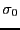 )。最初円盤の中心は原点にあり、やがてx方向に速さ
)。最初円盤の中心は原点にあり、やがてx方向に速さ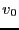 で動き始め
た。ただし、円盤は常にxy面上にある。動き始めた瞬間を考えよう。
で動き始め
た。ただし、円盤は常にxy面上にある。動き始めた瞬間を考えよう。
- 円盤が動くことによって電流が生じる。その面電流密度を求めよ。
- 円盤が動くことによって生じるベクトル・ポテンシャルを求めよ。
ただし、点
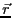 (
(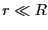 、
、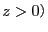 の点について調べれば良い。
の点について調べれば良い。
- 求めたベクトル・ポテンシャルから磁場を求めよ。
===== 解答 =====
- 面電荷が
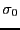 でx方向に速さ
でx方向に速さ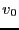 で動いているので、面電流密度
で動いているので、面電流密度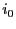 は
は
となる。
- ベクトル・ポテンシャルを表す式に代入すると
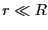 より
より
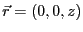 の場合のみを考えれば十分である。また、明ら
かにベクトル・ポテンシャルはy,z成分はゼロなので、x成分のみを考える。
の場合のみを考えれば十分である。また、明ら
かにベクトル・ポテンシャルはy,z成分はゼロなので、x成分のみを考える。
円筒座標を用いて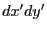 を
を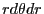 に置き換えると、
に置き換えると、
-
Administrator
平成25年7月6日