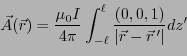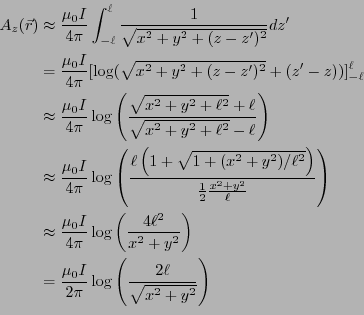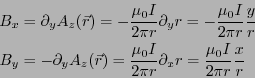: 問題2.7.3
: ベクトル・ポテンシャル
: 問題2.7.1
目次
非常に長い線分上を流れる電流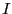 が点
が点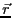 につくる
ベクトル・ポテンシャル
につくる
ベクトル・ポテンシャル
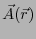 を求めよ。
線分は
を求めよ。
線分は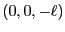 から
から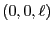 で、
で、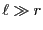 とする。また、このベ
クトル・ポテンシャルから得られる磁場を計算せよ。
とする。また、このベ
クトル・ポテンシャルから得られる磁場を計算せよ。
ヒント:
===== 解答 =====
ここで、
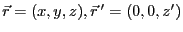 である。
である。
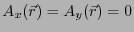 は明らかである。従って、以後
は明らかである。従って、以後
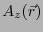 のみを考察する。
のみを考察する。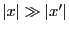 、
、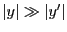 と
と
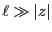 より、
より、
と近似できる。
ベクトル・ポテンシャルはz成分しかないから、
となる。ここで、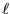 は定数としてその微分はゼロとしている。
は定数としてその微分はゼロとしている。
Administrator
平成25年7月6日