図1.3のような直交した3つの軸に平行な3つの単位ベクトル
![]() によって、
任意の3次元ベクトルが
によって、
任意の3次元ベクトルが
| (1.1) |
![]() をそれぞれ右手の
人差指、中指、親指に対応させるとき右手系の座標系を選んだと言う。
をそれぞれ右手の
人差指、中指、親指に対応させるとき右手系の座標系を選んだと言う。
![]() を数の組で
を数の組で
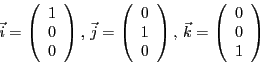
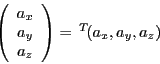
ベクトル![]() が位置ベクトルならば
が位置ベクトルならば![]() は長さの次
元を持つ量であるし、力を表すベクトルならば各成分は力の次元を持つ量である。
ベクトルの大きさは
は長さの次
元を持つ量であるし、力を表すベクトルならば各成分は力の次元を持つ量である。
ベクトルの大きさは
| (1.2) |
物理ではある物理量に対してよく使われる記号がある。
例えば、位置ベクトルに対しては![]() 、力に対しては
、力に対しては![]() 、速度に対
しては
、速度に対
しては![]() などである。また、ベクトル量とスカラー量を明確に区別する
ためにベクトルには必ず矢印
などである。また、ベクトル量とスカラー量を明確に区別する
ためにベクトルには必ず矢印 ![]() を用いる。
を用いる。