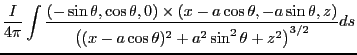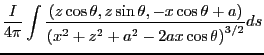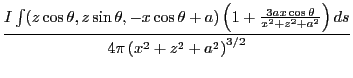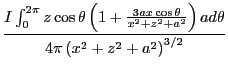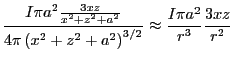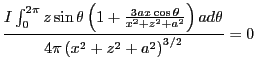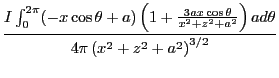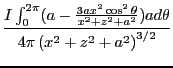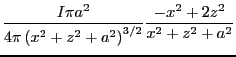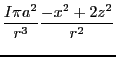: アンペールの法則
: 電流と静磁場
: 問題2.6.9
目次
中心が原点で、
半径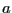 の円形回路に電流
の円形回路に電流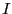 が流れている。回路によって決まる法線ベクトルを
が流れている。回路によって決まる法線ベクトルを
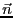 とすると、十分遠方
とすると、十分遠方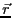 (
(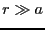 )での磁場の強さ(磁界)は
以下の式で表すことができる。
)での磁場の強さ(磁界)は
以下の式で表すことができる。
ここで、
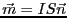 (
( は回路の面積。ここでは
は回路の面積。ここでは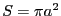 )はこの電流による磁気モーメントである2.2。
)はこの電流による磁気モーメントである2.2。
計算を簡単にするために、
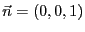 とし、
とし、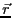 はxz面内のみを
考えて、
はxz面内のみを
考えて、
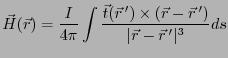 を計算する。
ただし、
を計算する。
ただし、
として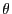 を
を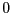 から
から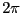 まで積分する。
まで積分する。
以後は成分毎に検討しよう。
得られた近似式は式2.75に
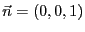 を代入したもの
になっている。また、z軸周りに回転することによって、y成分が0でない場合も
求めることができる。
を代入したもの
になっている。また、z軸周りに回転することによって、y成分が0でない場合も
求めることができる。




: アンペールの法則
: 電流と静磁場
: 問題2.6.9
目次
Administrator
平成25年7月6日
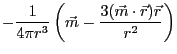
![]() とし、
とし、![]() はxz面内のみを
考えて、
はxz面内のみを
考えて、
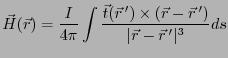 を計算する。
ただし、
を計算する。
ただし、