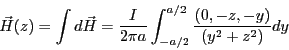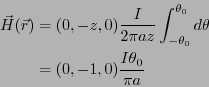: 円電流による磁気モーメント
: ビオ-サバールの法則
: 問題2.6.8
目次
長さが無限と見なせる幅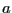 の薄い平らな導体板(xy面内にあり,幅はy方向とする)に
電流
の薄い平らな導体板(xy面内にあり,幅はy方向とする)に
電流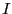 が流れている。電流密度は一様である。
板の中央線上の任意の点を原点とし,z軸上の点
が流れている。電流密度は一様である。
板の中央線上の任意の点を原点とし,z軸上の点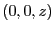 における磁界を求めよ。
における磁界を求めよ。
===== 解答 =====
この導体を流れる電流を点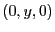 を通るx軸に沿った無限に長い電流を
を通るx軸に沿った無限に長い電流を
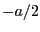 から
から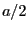 まで積分すれば良い。
問題2.6.6より,z軸上の点
まで積分すれば良い。
問題2.6.6より,z軸上の点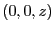 の磁界の大きさは
の磁界の大きさは
である。向きまで考慮すると
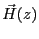 は
は
となり,z成分の被積分関数が奇関数の寄与は0になる。
また、
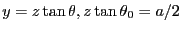 とおくと、
とおくと、
となる。
Administrator
平成25年7月6日
![]() を通るx軸に沿った無限に長い電流を
を通るx軸に沿った無限に長い電流を
![]() から
から![]() まで積分すれば良い。
問題2.6.6より,z軸上の点
まで積分すれば良い。
問題2.6.6より,z軸上の点![]() の磁界の大きさは
の磁界の大きさは
![]() は
は