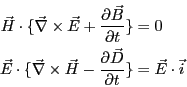
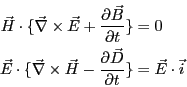
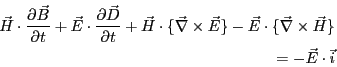
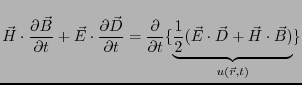 |
(3.24) |
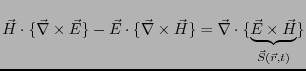 |
(3.25) |
各項の意味を考えてみよう。静電界のエネルギー密度は
![]() で、静磁場のエネルギー密度は
で、静磁場のエネルギー密度は
![]() (式3.14参照)で表された。
これらの式が時間変動する電界、磁場にも適用できると考えると、
(式3.14参照)で表された。
これらの式が時間変動する電界、磁場にも適用できると考えると、![]() は
電界と磁場、
すなわち電磁場のエネルギー密度を表していることになる。
は
電界と磁場、
すなわち電磁場のエネルギー密度を表していることになる。
右辺の
![]() は単位体積中の荷電粒子が電界から受ける単位時間当た
りの仕事である。ローレンツ力は荷電粒子の運動方向と垂直に作用するので、磁
場は荷電粒子に仕事をしないことを考えると、右辺は単位体積中の荷電粒子が電
磁場から受ける単位時間当たりの仕事になる。電磁場から考えるとそれだけのエ
ネルギーが電磁場から、なくなっていくことを示している。
は単位体積中の荷電粒子が電界から受ける単位時間当た
りの仕事である。ローレンツ力は荷電粒子の運動方向と垂直に作用するので、磁
場は荷電粒子に仕事をしないことを考えると、右辺は単位体積中の荷電粒子が電
磁場から受ける単位時間当たりの仕事になる。電磁場から考えるとそれだけのエ
ネルギーが電磁場から、なくなっていくことを示している。
![]() の意味を考えるに当たって、式3.30と式3.27の
類似性に注目しよう。式3.30の
の意味を考えるに当たって、式3.30と式3.27の
類似性に注目しよう。式3.30の![]() と式3.27と
と式3.27と
![]() が対応している。そのように考えると、
が対応している。そのように考えると、![]() は電磁場のエ
ネルギーの流れに相当することがわかる。この式を導きだした人の名前をとって、
このベクトルはポインティング・ベクトル(Poynting vector)と呼ばれて
いる3.1。
は電磁場のエ
ネルギーの流れに相当することがわかる。この式を導きだした人の名前をとって、
このベクトルはポインティング・ベクトル(Poynting vector)と呼ばれて
いる3.1。