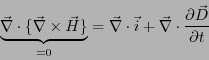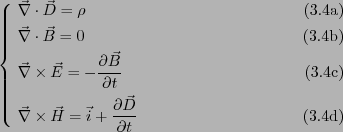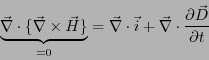微分形

物理現象を近接作用の観点から理解しようとしたとき、物理法則を微分形で表現 したほうが理解しやすい。マクスウェルの方程式の微分形は、 ガウスの定理とストークスの定理を用いると、先のマクスウェルの 方程式を次のような微分形で表すことができる。

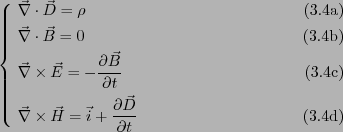
式3.26dの両辺の発散をとると、左辺は恒等的にゼロになる。

$$\begin{eqnarray*} \underbrace{\vec{\nabla}\cdot \{\vec{\nabla}\times \vec{H} \}}... ...ec{i} + \vec{\nabla}\cdot \frac{\partial \vec{D}}{\partial t} \end{eqnarray*}$$

ここに、時間微分と空間微分を入れ替えて式3.26aを代入すると、

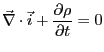$$\vec{\nabla}\cdot \vec{i} + \frac{\partial \rho}{\partial t} =0$$ (3.23)

となる。この式は電荷が保存されることを意味している。すなわち、電荷密度が 変化するときには、それに見合った電流が流れ込んでいることを示している。