



: 電磁場のエネルギー
: マクスウェルの方程式
: 微分形
目次
マクスウェルの方程式にあらわれる変数は、電界と磁場のの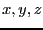 方向の成分
で計6こである。一方、マクスウェルの方程式は成分に分解すると、計8こあるよ
うにみえる。この点について考察しよう。
方向の成分
で計6こである。一方、マクスウェルの方程式は成分に分解すると、計8こあるよ
うにみえる。この点について考察しよう。
式3.26dの両辺の発散をとると、左辺は恒等的にゼロになる。
次に、式3.27を用いて、
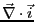 を消去し、
を消去し、
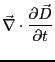 は
は
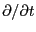 と
と
 の順序を入れ替えると、
の順序を入れ替えると、
となる。言い換えると、ある関数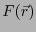 を用いて、
を用いて、
となる。これは、初期条件として、式3.26aが成立するならば、その後電
磁場が変化しても、常に式3.26aが成立することを意味している。よって、
式3.26aは式の数と変数の数を検討するときに、考えなくてよい。同様の
ことが式3.26bにも成立するので、変数6こに対して式が6こあることになる。
Administrator
平成25年7月6日
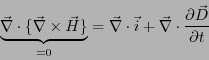
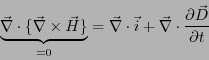
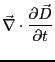 は
は