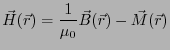: 静磁場の基本法則のまとめ
: 物質中の電界と磁場
: 磁性体
目次
長岡の電磁気学IIでは、磁化電流を導入してアンペールの法則から物質中
の静磁場の基本法則を「導出」している。この磁化電流の起源は曖昧なので、以
下のように、静磁場の基本法則を考えることにする。
物質中では磁化が存在する場合もあるので、直接磁束密度と電流密度を結びつけ
ることはできない。そこで、磁束密度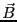 から磁化
から磁化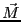 の効果を差し
引いた磁界
の効果を差し
引いた磁界
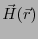 を
を
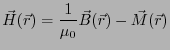 |
|
|
(3.37) |
と定義して、形式的に
が成立するようにする。ここで、
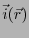 は磁化電流ではない「本当」
の電流である。
3.2
は磁化電流ではない「本当」
の電流である。
3.2
強磁性体ではない通常の磁性体では、
弱い磁場の下で磁化ベクトルはかけられた磁場に比例する。そこで、
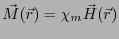 |
|
|
(3.38) |
と表し、磁化率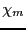 を定義する。磁束密度と磁界の間には
を定義する。磁束密度と磁界の間には
という関係が成り立つ。ここで、
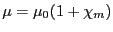 を透磁率と言う。
通常の物質では
を透磁率と言う。
通常の物質では
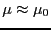 と考えて良いことがほとんどである。この
点が誘電率
と考えて良いことがほとんどである。この
点が誘電率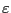 と大きく異なる。
と大きく異なる。
Administrator
平成25年7月6日
![]() から磁化
から磁化![]() の効果を差し
引いた磁界
の効果を差し
引いた磁界
![]() を
を