



: 問題2.4.7
: 導体
: 問題2.4.6
目次
ある導体に電荷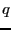 を帯電させた時、その導体表面の電位が
無限遠点を基準に
を帯電させた時、その導体表面の電位が
無限遠点を基準に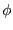 になったとする。この時、この導体の
静電容量
になったとする。この時、この導体の
静電容量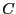 は
は
で与えられる。その単位にはC/Vを用い、Fと略記してファラッドと
呼ぶ。静電容量は導体を帯電させるのに必要な
エネルギーが小さいほど大きくなる。また、その時のエネルギーは
となる。
導体が多数ある場合には、お互いに影響を及ぼしあう。
導体1の電位を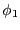 、導体2の電位を0とした場合に、
それぞれの導体の持つ電荷を
、導体2の電位を0とした場合に、
それぞれの導体の持つ電荷を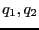 とすれば、
とすれば、
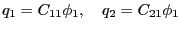 |
|
|
(2.48) |
となる。導体1の電位を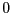 、導体2の電位を
、導体2の電位を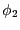 とした場合に、
それぞれの導体の持つ電荷を
とした場合に、
それぞれの導体の持つ電荷を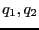 とすれば、
とすれば、
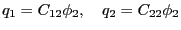 |
|
|
(2.49) |
となる。導体1,2の電位がそれぞれ
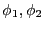 の場合には
重ね合わせになるので、
の場合には
重ね合わせになるので、
となる。
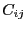 は導体の形状や位置関係で決まるが、必ず
は導体の形状や位置関係で決まるが、必ず
となる。この関係を容量係数の相反定理と呼ぶ。




: 問題2.4.7
: 導体
: 問題2.4.6
目次
Administrator
平成25年7月6日
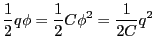
![]() 、導体2の電位を0とした場合に、
それぞれの導体の持つ電荷を
、導体2の電位を0とした場合に、
それぞれの導体の持つ電荷を![]() とすれば、
とすれば、
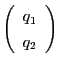
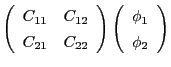
![]() は導体の形状や位置関係で決まるが、必ず
は導体の形状や位置関係で決まるが、必ず