: 問題2.4.9
: 静電容量
: 問題2.4.7
目次
導体が2個ある場合について、相反定理を以下の手順で証明せよ。
- 電荷
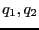 が与えられた時の
が与えられた時の
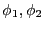 を求めよ。
を求めよ。
を解けば良い。
-
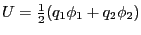 より
系全体のエネルギーを求めよ。
より
系全体のエネルギーを求めよ。
- 導体1の電荷を微少量
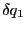 だけ変化させた時のエネルギーの変化
だけ変化させた時のエネルギーの変化
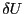 を求めよ。ただし、
を求めよ。ただし、
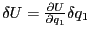 を用いる。
を用いる。
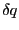 を微少と考えれば、その電荷変化による電位変化は
を微少と考えれば、その電荷変化による電位変化は
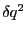 の程度となり、無視できる。従って、
の程度となり、無視できる。従って、
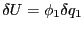 として、良いはずである。
上と比較することによって、相反定理が成り立つことを示せ。
として、良いはずである。
上と比較することによって、相反定理が成り立つことを示せ。
===== 解答 =====
-
- 上で求めた
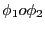 を代入すれば、
を代入すれば、
-
-
は先に計算した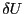 と等しい。従って、
と等しい。従って、
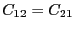 でなければな
らない。
でなければな
らない。
Administrator
平成25年7月6日