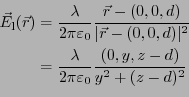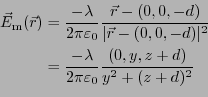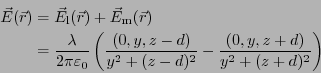: 静電容量
: 境界値問題
: 問題2.4.5
目次
平らな導体の表面から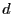 だけ離れた所に置かれた直線状の電荷がある。その線
電荷密度は
だけ離れた所に置かれた直線状の電荷がある。その線
電荷密度は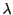 である。電場を求めよ。また、導体表面に生じる電荷密度を求めよ。
である。電場を求めよ。また、導体表面に生じる電荷密度を求めよ。
===== 解答 =====
直線状の電荷は点電荷が線上に分布していると考える。それぞれの電荷の鏡像は
先の問題と同様に考えることができる。また、無限に長い直線状の電荷を考えて
いるので、電場を求めるのは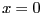 の位置だけで十分である。
の位置だけで十分である。
直線状の電荷による電場の大きさ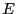 はガウスの法則より、
はガウスの法則より、
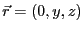 では
では
となる。向きも考慮すると、
となる。同様に鏡像による電場
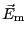 は
は
となる。従って、電場は、
特に、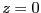 では
では
となる。従って、表面電荷密度は
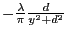 となる。
となる。
Administrator
平成25年7月6日
![]() の位置だけで十分である。
の位置だけで十分である。
![]() はガウスの法則より、
はガウスの法則より、
![]() では
では