



: 問題2.4.4
: 導体
: 問題2.4.3
目次
電荷の分布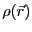 が与えられている場合に電場を求めるには
この電荷密度に対してポアソン方程式を解けばよい。しかし、導体が存在
すると、その表面の電荷密度は表面の電位を一定にするように決定される。
言い換えると、与えられた電荷密度と導体の表面で値が一定(境界値が一定)
という条件の下でポアソン方程式を解く必要がある。このような問題を境界値
問題と言う。
が与えられている場合に電場を求めるには
この電荷密度に対してポアソン方程式を解けばよい。しかし、導体が存在
すると、その表面の電荷密度は表面の電位を一定にするように決定される。
言い換えると、与えられた電荷密度と導体の表面で値が一定(境界値が一定)
という条件の下でポアソン方程式を解く必要がある。このような問題を境界値
問題と言う。
境界値問題には以下のような重ね合わせの原理が成り立つ。真空中に導体1,2が
置かれている。無限遠における電位を0として、導体1の電位を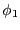 、導体2
の電位を0としたときの境界値問題の解を
、導体2
の電位を0としたときの境界値問題の解を
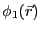 とする。同様に
導体1の電位を0、導体2の電位を
とする。同様に
導体1の電位を0、導体2の電位を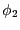 としたときの境界値問題の解を
としたときの境界値問題の解を
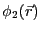 とする。導体1,2の電位がそれぞれ
とする。導体1,2の電位がそれぞれ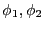 の
場合の境界値問題の解は
の
場合の境界値問題の解は
となる。なぜならば、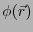 は真空中でラプラス方程式を満たす。
一方、導体1の表面では
は真空中でラプラス方程式を満たす。
一方、導体1の表面では
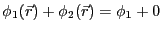 なので、
なので、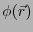 は境界条件を満たす。導体2の表面上でも同様である。
境界値問題の解は一つしかないから、これが求める解になる。
は境界条件を満たす。導体2の表面上でも同様である。
境界値問題の解は一つしかないから、これが求める解になる。
Administrator
平成25年7月6日
![]() 、導体2
の電位を0としたときの境界値問題の解を
、導体2
の電位を0としたときの境界値問題の解を
![]() とする。同様に
導体1の電位を0、導体2の電位を
とする。同様に
導体1の電位を0、導体2の電位を![]() としたときの境界値問題の解を
としたときの境界値問題の解を
![]() とする。導体1,2の電位がそれぞれ
とする。導体1,2の電位がそれぞれ![]() の
場合の境界値問題の解は
の
場合の境界値問題の解は