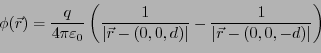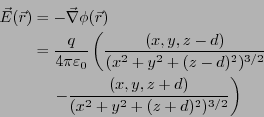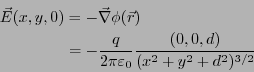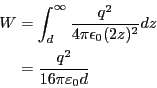: 問題2.4.5
: 境界値問題
: 境界値問題
目次
平らな導体の表面から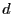 だけ離れた所に置かれた点電荷
だけ離れた所に置かれた点電荷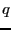 による電場と導体に
静電誘導される表面電荷密度を以下の手順に従って求めよ。
による電場と導体に
静電誘導される表面電荷密度を以下の手順に従って求めよ。
- 点電荷の近傍では電気力線は放射状に、そして導体の表面には電気力線は
垂直に入射することに注意して、全空間での電気力線の様子を描け。
- 導体表面を鏡面と見立てたときの点電荷
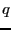 の像の位置に
の像の位置に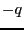 の電荷を置
き、この二つの電荷による電気力線の様子を描け。ただし、導体の存在は
無視する
の電荷を置
き、この二つの電荷による電気力線の様子を描け。ただし、導体の存在は
無視する
- 2番目の場合の金属の外の電位を求めよ。
- 点電荷
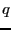 を無限遠まで引き離すために必要な仕事を求めよ。
を無限遠まで引き離すために必要な仕事を求めよ。
===== 解答 =====
- 省略。
- 省略。
- 電位
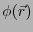 は
は
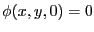 になっており、金属表面が等電位面になっている。
になっており、金属表面が等電位面になっている。
電場は
特に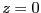 では、
では、
となる。従って、表面電荷密度は
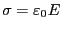 より求まる。
より求まる。
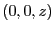 にある点電荷に働く力は、鏡像との間に働く力より計算でき、
にある点電荷に働く力は、鏡像との間に働く力より計算でき、
である。これに抗して電荷を動かさないといけない。従って、必要な仕事は
となる。
Administrator
平成25年7月6日