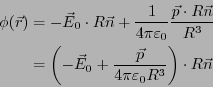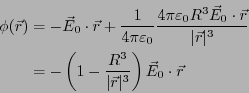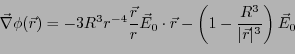: 問題2.4.6
: 境界値問題
: 問題2.4.4
目次
一様な静電場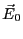 の中に帯電してない半径
の中に帯電してない半径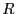 の導体球を置いた。
静電場はどのようになるか?
の導体球を置いた。
静電場はどのようになるか?
- 一様な静電場を作る電位は、
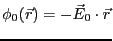 であることを確認せよ。
であることを確認せよ。
- 電気双極子による電位は
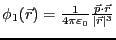 である。一様な
電場を作る電位と電気双極子が作る電位が球の表面上で0になる条件は何
か?
である。一様な
電場を作る電位と電気双極子が作る電位が球の表面上で0になる条件は何
か?
- 導体球の外側の電位を求めよ。
- 導体球の表面の電荷密度を求めよ。
- この表面の電荷分布と同じ電荷分布を絶縁体球上に再現した。この電荷分
布によって得られる電場を考察せよ。
===== 解答 =====
- 省略。
- 合成した電位は、
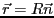 の位置で、
の位置で、
となる。ただし、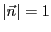 とする。
従って、
とする。
従って、
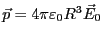 が条件となる。
が条件となる。
-
となる。
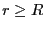 において、
において、
となる。
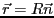 のとき、
のとき、
となる。従って、電荷密度はこれを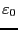 倍すれば良い。
倍すれば良い。
- 導体球内部では、この電荷密度による電場と外場によって導体球の内部
の電場は0になっていた。従って、この電荷密度による電場は外場と反対向き、
すなわち
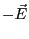 となる。一方、球外部では原点に
となる。一方、球外部では原点に
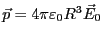 という電気双極子がある場合の電
場になる。
という電気双極子がある場合の電
場になる。
Administrator
平成25年7月6日