



: 境界値問題
: 導体と絶縁体
: 問題2.4.2
目次
導体の平らな表面の深さ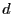 まで電荷が一様な密度
まで電荷が一様な密度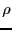 で分布している。
で分布している。
- 表面からの深さが
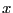 の導体内部の電場の強さ
の導体内部の電場の強さ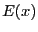 を求めよ。
を求めよ。
- 表面電荷に働く力は単位面積あたり、
で与えられる。計算せよ。
===== 解答 =====
- 導体表面に垂直にx軸を取り、正の向きを導体に入る方向に取る。
原点は導体表面に取る。電場は
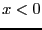 で
で
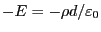 、
、
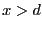 で0である。
で0である。
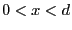 ではガウスの法則により、
ではガウスの法則により、
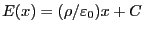 となるはずである。ここで
となるはずである。ここで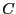 は導体の内外で電位が連続になるように
するための定数。
は導体の内外で電位が連続になるように
するための定数。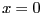 で連続であるために、
で連続であるために、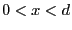 で
で
となる。
-
符号は負なので、力は導体外向きに働く。
Administrator
平成25年7月6日