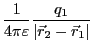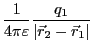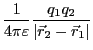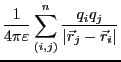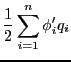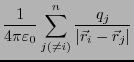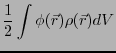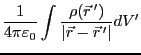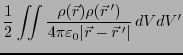: 問題2.2.15
: 電場の性質
: 問題2.2.14
目次
点電荷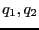 がそれぞれ位置
がそれぞれ位置
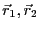 に存在する。
電荷
に存在する。
電荷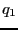 による電荷
による電荷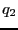 の位置におけるポテンシャルは、
の位置におけるポテンシャルは、
である。従って、二つの電荷が存在することによる(静電)エネルギーは
となる。複数の電荷が存在する場合には以下のように拡張すればよい。
ここで、
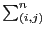 はn個の電荷のすべての組み合わせについて足しあげ
ることを意味する。また、以下のように表すこともできる。
はn個の電荷のすべての組み合わせについて足しあげ
ることを意味する。また、以下のように表すこともできる。
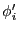 は電荷
は電荷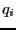 以外の電荷から生じる電位である。ここで
以外の電荷から生じる電位である。ここで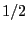 は2回足し
あわせてしまっているので、それを補正するためである。より一般には、
は2回足し
あわせてしまっているので、それを補正するためである。より一般には、
となる。あるいは、
とあらわすこともできる。




: 問題2.2.15
: 電場の性質
: 問題2.2.14
目次
Administrator
平成25年7月6日