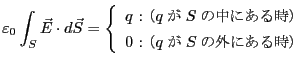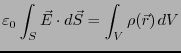: 問題2.2.7
: 電場の性質
: 問題2.2.6
目次
ガウスの法則
ガウスの法則を理解するために、立体角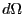 を
定義しておこう。ある面
を
定義しておこう。ある面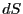 を原点から見た時の
立体角
を原点から見た時の
立体角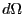 は
は
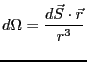 |
|
|
(2.7) |
である。
ただし、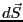 は大きさが
は大きさが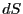 で方向はこの
面に垂直で外向きのベクトルである。
例えば、原点を中心とする半径
で方向はこの
面に垂直で外向きのベクトルである。
例えば、原点を中心とする半径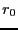 の球の原点から
見込んだ立体角は球の表面積が
の球の原点から
見込んだ立体角は球の表面積が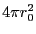 だから
それを
だから
それを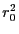 で割って
で割って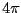 になる。
になる。
原点に電荷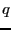 があり、その周りを閉曲面
があり、その周りを閉曲面 が囲んでいる。その閉曲面上
で
が囲んでいる。その閉曲面上
で
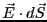 を積分すると、
を積分すると、
また、閉曲面 が電荷
が電荷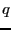 を取り囲んでいない場合には
を取り囲んでいない場合には
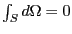 になるので
になるので
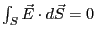 になる。以上まとめると、
になる。以上まとめると、
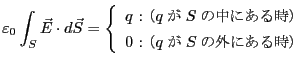 |
|
|
(2.9) |
一般の電荷分布の場合には、
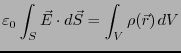 |
|
|
(2.10) |
となる。ただし、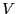 は閉曲面
は閉曲面 で囲まれた体積である。
で囲まれた体積である。
Administrator
平成25年7月6日
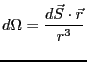
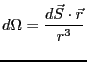
![]() があり、その周りを閉曲面
があり、その周りを閉曲面![]() が囲んでいる。その閉曲面上
で
が囲んでいる。その閉曲面上
で
![]() を積分すると、
を積分すると、
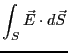
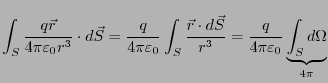
![]() が電荷
が電荷![]() を取り囲んでいない場合には
を取り囲んでいない場合には
![]() になるので
になるので
![]() になる。以上まとめると、
になる。以上まとめると、