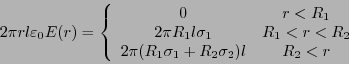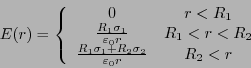: 問題2.2.11
: ガウスの法則
: 問題2.2.9
目次
半径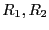 の無限に長い二つの円筒に電荷が、それぞれ
面電荷密度
の無限に長い二つの円筒に電荷が、それぞれ
面電荷密度
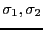 で一様に分布している。
二つの円筒の軸が一致している場合に、生じる電場を求めよ。
で一様に分布している。
二つの円筒の軸が一致している場合に、生じる電場を求めよ。
===== 解答 =====
対称性から電場は円筒の軸から放射状に生じ、その大きさは軸からの距離のみに
依存する。閉曲面として、円筒と軸が同じで半径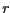 ながさ
ながさ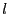 の円筒を考える。
円筒の上下の面に垂直な磁場は存在しないので、側面のみに注目してガウスの法
則を適用すれば良い。
の円筒を考える。
円筒の上下の面に垂直な磁場は存在しないので、側面のみに注目してガウスの法
則を適用すれば良い。
従って、電場は
となる。
Administrator
平成25年7月6日
![]() ながさ
ながさ![]() の円筒を考える。
円筒の上下の面に垂直な磁場は存在しないので、側面のみに注目してガウスの法
則を適用すれば良い。
の円筒を考える。
円筒の上下の面に垂直な磁場は存在しないので、側面のみに注目してガウスの法
則を適用すれば良い。