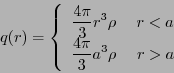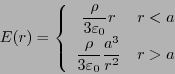: 問題2.2.8
: ガウスの法則
: ガウスの法則
目次
半径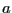 の球内に一様な電荷密度
の球内に一様な電荷密度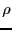 (正)で電荷が分布している場合
の電場を求めよ。ガウスの法則を用いても良い。
(正)で電荷が分布している場合
の電場を求めよ。ガウスの法則を用いても良い。
===== 解答 =====
対称性より同心球面 上ではすべての電場の大きさは一定で、
その方向は球面に垂直で外向きである。その大きさはその球面
の半径だけの関数であるから、
上ではすべての電場の大きさは一定で、
その方向は球面に垂直で外向きである。その大きさはその球面
の半径だけの関数であるから、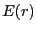 とする。この球面上で
ガウスの法則を適用すると、
とする。この球面上で
ガウスの法則を適用すると、
一方、この球面 内にある電荷の総和
内にある電荷の総和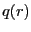 は、
以下の式で表されるので、
は、
以下の式で表されるので、
となる。ガウスの法則とあわせて、
が得られる。
Administrator
平成25年7月6日
![]() 上ではすべての電場の大きさは一定で、
その方向は球面に垂直で外向きである。その大きさはその球面
の半径だけの関数であるから、
上ではすべての電場の大きさは一定で、
その方向は球面に垂直で外向きである。その大きさはその球面
の半径だけの関数であるから、![]() とする。この球面上で
ガウスの法則を適用すると、
とする。この球面上で
ガウスの法則を適用すると、