



: 問題2.6.1
: 電流と静磁場
: 磁場中の磁石
目次
ある点において磁束密度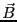 がある。そこを
荷電粒子
がある。そこを
荷電粒子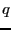 が速度
が速度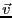 で通過する場合、その荷電粒子には
「ローレンツ力」
で通過する場合、その荷電粒子には
「ローレンツ力」
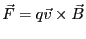 |
|
|
(2.68) |
が働く。ローレンツ力は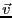 に直交しており、磁束密度の下で
荷電粒子が運動しても速さ(エネルギー)の変化は起きない。
に直交しており、磁束密度の下で
荷電粒子が運動しても速さ(エネルギー)の変化は起きない。
さらに、電場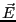 がある場合には、荷電粒子は
がある場合には、荷電粒子は
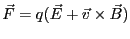 |
|
|
(2.69) |
の力を受ける。さて、この粒子と一緒に動きながら粒子を観測しよう。
運動する観測者からは
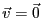 である。言い換えると磁束密度
からの力は存在しない。しかし、粒子に作用する
力は観測者の運動にかかわらず同じはずである。観測者にとっては、
粒子のところに
である。言い換えると磁束密度
からの力は存在しない。しかし、粒子に作用する
力は観測者の運動にかかわらず同じはずである。観測者にとっては、
粒子のところに
の電場があるように見える。電場と磁場(磁束密度)は別の
ものではなく、観測の仕方によって相互に変換されるものである。
磁束密度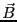 の中に置かれた電流
の中に置かれた電流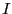 が流れる長さ
が流れる長さ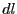 の導線に
働く力
の導線に
働く力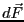 は、電流が導線の中の荷電粒子の
運動であることから、ローレンツ力によって理解できる。
導線の方向を
は、電流が導線の中の荷電粒子の
運動であることから、ローレンツ力によって理解できる。
導線の方向を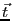 として、
として、
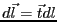 と表すことにすれば、
と表すことにすれば、
となる。
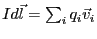 であることに注意。
ここで、和は長さ
であることに注意。
ここで、和は長さ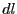 の導線中の電流を担う荷電粒子に対して行う。
この法則を「フレミングの左手の法則」と言う。
の導線中の電流を担う荷電粒子に対して行う。
この法則を「フレミングの左手の法則」と言う。
図 2.12:
![\includegraphics[bb=0 530 380 830,width=6cm]{fig77.eps}](img808.png) |
Administrator
平成25年7月6日
![]() がある場合には、荷電粒子は
がある場合には、荷電粒子は
![]() の中に置かれた電流
の中に置かれた電流![]() が流れる長さ
が流れる長さ![]() の導線に
働く力
の導線に
働く力![]() は、電流が導線の中の荷電粒子の
運動であることから、ローレンツ力によって理解できる。
導線の方向を
は、電流が導線の中の荷電粒子の
運動であることから、ローレンツ力によって理解できる。
導線の方向を![]() として、
として、
![]() と表すことにすれば、
と表すことにすれば、