



: 問題2.6.5
: ローレンツ力
: 問題2.6.3
目次
一辺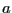 の小さな正方形の回路に電流
の小さな正方形の回路に電流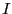 が流れている。この正方形はxy面内に
あり、xy面には垂直にしかし大きさは一様ではない磁場がかかっている。
この磁場の磁束密度の位置依存性が
が流れている。この正方形はxy面内に
あり、xy面には垂直にしかし大きさは一様ではない磁場がかかっている。
この磁場の磁束密度の位置依存性が
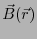 と表されるとして、
回路に働く力を求めよ。ただし、
と表されるとして、
回路に働く力を求めよ。ただし、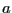 は磁束密度の変化の特徴的な長さに比べて
十分小さいものとする。また、正方形の各辺は軸に平行であるとする。
は磁束密度の変化の特徴的な長さに比べて
十分小さいものとする。また、正方形の各辺は軸に平行であるとする。
===== 解答 =====
xy面内の点
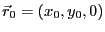 の近傍で、磁場は以下のように近似で
きる。
の近傍で、磁場は以下のように近似で
きる。
y軸に平行な2辺に働く力はx軸方向になり、それぞれ
である。従って、その合力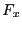 は
は
となる。同様にx軸に平行な2辺に働く力はy方向に働く力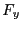 となり、
となり、
となる。
Administrator
平成25年7月6日
![]() の近傍で、磁場は以下のように近似で
きる。
の近傍で、磁場は以下のように近似で
きる。
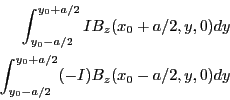
![\begin{eqnarray*}
F_x &=&
I \left(B_z(x_0, y_0, 0)+\partial_x B_z(x_0, y_0, 0)...
...t)a \\
&=& I [\partial_x B_z(\vec{r})]_{\vec{r}=\vec{r}_0} a^2
\end{eqnarray*}](img835.png)