問題2.6.5

導体に電流を流しながら、電流に垂直に磁場をかけると、 電流、磁場両方に垂直な方向に電場が生じる。この現象を ホール効果という。ホール効果による電場は

$$\vec{E} = -\frac{\vec{i} \times \vec{B}}{nq}$$

となることを確かめよ。ここで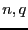$n, q$は伝導を担う粒子の密度とその電荷である。

===== 解答 =====

磁束密度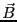$\vec{B}$の磁場から電流密度 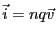$\vec{i}= n q \vec{v}$を 担っている荷電粒子に働くローレンツ力は

$$\begin{eqnarray*} \vec{F} &=& q \vec{v}\times \vec{B} \end{eqnarray*}$$

である。定常状態では電流の向きに直交した方向の力は誘起される電場とキャン セルしなければならないので、その電場を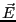$\vec{E}$とすると、

$$\begin{eqnarray*} \vec{0} &=& q \left(\vec{E} + \vec{v} \times \vec{B}\right) \end{eqnarray*}$$

である。従って、

$$\begin{eqnarray*} \vec{E} &=& - \vec{v} \times \vec{B} = - \frac{\vec{i} \times \vec{B}}{nq} \end{eqnarray*}$$

電荷の正負に応じて電場の向きが変化することに注意。