サイクロトロン運動:
紙面に対して垂直上向き(z方向)に磁束密度
![]() のある空間に、速度
のある空間に、速度
![]() の粒子(電荷
の粒子(電荷![]() 、質量
、質量![]() )
が入射した。
この荷電粒子に対するローレンツ力は常に進行方向に
対して垂直で大きさが
)
が入射した。
この荷電粒子に対するローレンツ力は常に進行方向に
対して垂直で大きさが![]() である。磁場による
ローレンツ力は仕事をしないので、
「運動エネルギー(
である。磁場による
ローレンツ力は仕事をしないので、
「運動エネルギー(
![]() )は一定
=速さは一定」である。すなわち、荷電粒子は「等速円運動」を行う。
この円運動の半径を求めよ。また、周期を求めよ。
)は一定
=速さは一定」である。すなわち、荷電粒子は「等速円運動」を行う。
この円運動の半径を求めよ。また、周期を求めよ。
===== 解答 =====
この円運動の半径![]() を求めよう。角速度
を求めよう。角速度![]() は
は
![]() である。
等速円運動において中心方向の加速度
である。
等速円運動において中心方向の加速度![]() は
は
![]() である。これは、ローレンツ力によって
生じているので、
である。これは、ローレンツ力によって
生じているので、
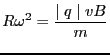 。
以上により、半径
。
以上により、半径![]() と周期
と周期
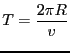 は以下のようになる。
は以下のようになる。
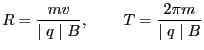 |
(2.71) |