研究内容

1. リサージェンス理論に基づく量子非摂動効果の研究


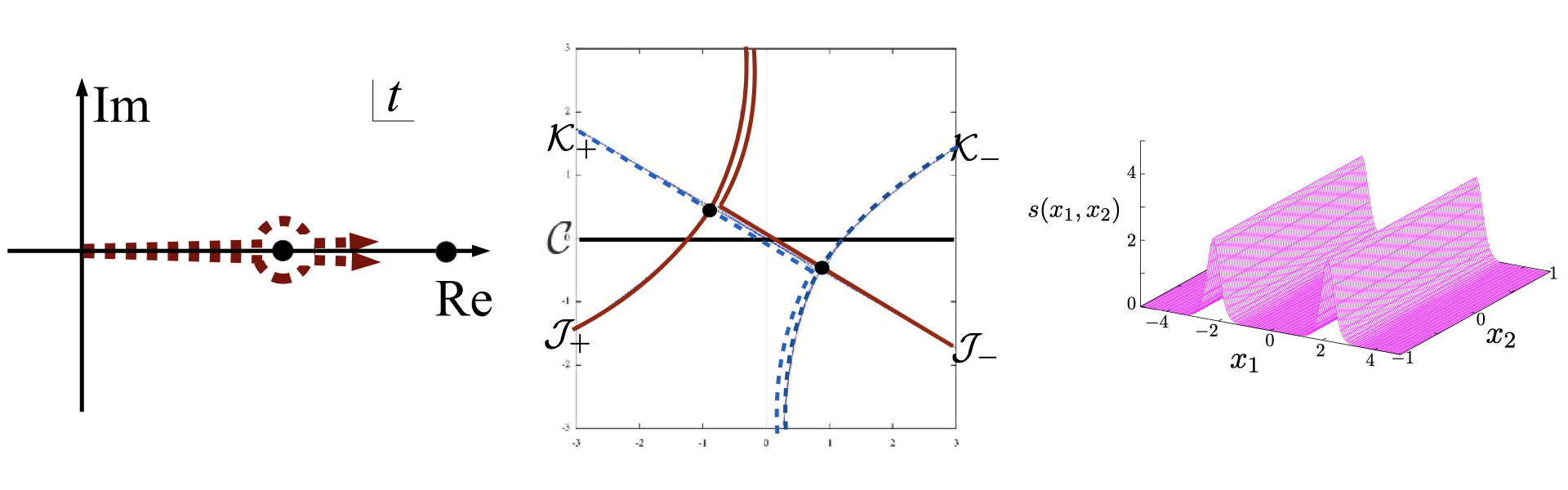
微小世界を記述する量子論においては，しばしば摂動計算と呼ばれる漸近展開に基づく計算手法が用いられます．特に素粒子現象を記述する場の量子論では大変重要になりますが，摂動級数は一般に発散するため，大部分のパラメータ領域の解析が出来ません．近年，ボレル和とストークス現象と呼ばれる数学的な概念を通して，その発散が実は摂動計算では記述出来ないとされる「非摂動現象」の情報を含む可能性(リサージェンス構造)が指摘されています．本研究室では，量子力学系，2次元シグマ模型，3次元超対称チャーン・サイモン理論，4次元QCD型理論について摂動級数と非摂動効果との関係を調べています．

関係する主な業績：
H.Nishimura, T.Fujimori, T.Misumi, M.Nitta, N.Sakai, JHEP06(2022)151
T.Fujimori, M.Honda, S.Kamata, T.Misumi, N.Sakai, T.Yoda PTEP02(2021)103B04
N.Sueishi, S.Kamata, T.Misumi, M.Unsal, JHEP12(2020)114
T.Fujimori, S.Kamata, T.Misumi, M.Nitta, N.Sakai, JHEP02(2019)190
T.Fujimori, M.Honda, S.Kamata, T.Misumi, N.Sakai, PTEP(2018)123B03
T.Fujimori, S.Kamata, T.Misumi, M.Nitta, N.Sakai, PRD94,105002(2016)
T.Misumi, M.Nitta, N.Sakai, JHEP09(2015)157
T.Misumi, M.Nitta, N.Sakai, JHEP06(2014)164
三角樹弘,「摂動級数の発散と非摂動効果:リサージェンス理論の量子論への応用」数理科学 2016年9月号

左図：摂動級数のボレル変換から不定虚部が現れる様子．中央図：不定虚部が非摂動的情報を与えるストークス現象．右図：複合ソリトン配位(非摂動効果)

2. コンパクト化時空上のゲージ理論の相構造と閉じ込め


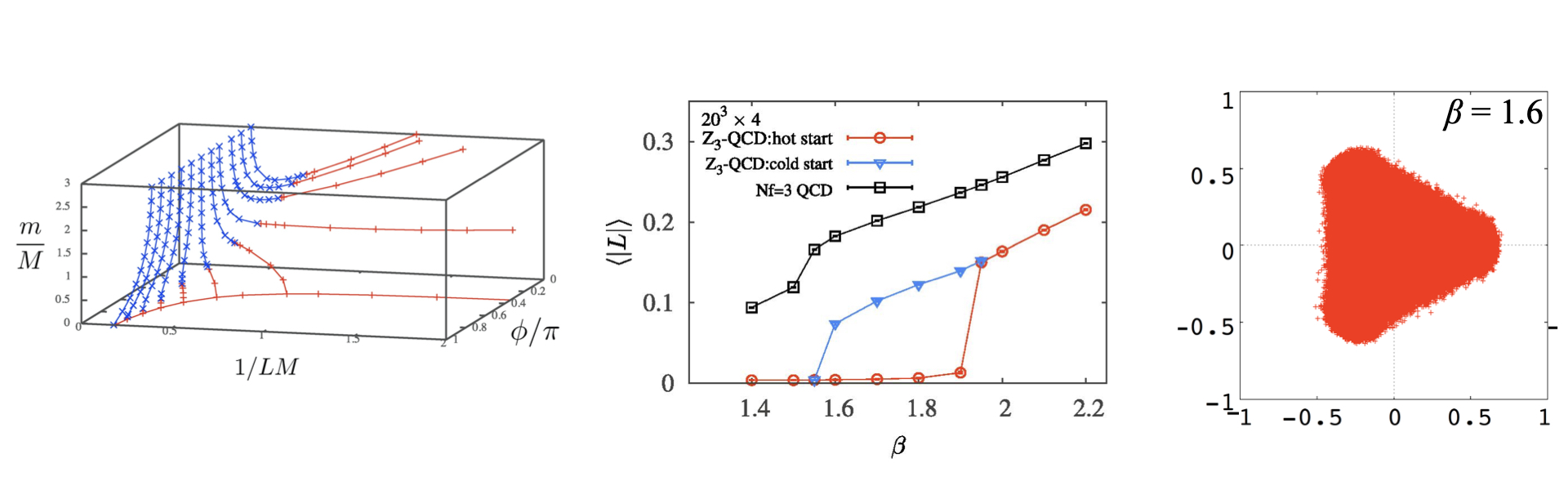
コンパクト化された次元を持つ空間に定義されたゲージ理論においてはしばしばゲージ対称性の自発的破れ等の興味深い現象が生じるだけでなく，コンパクト化半径が十分小さい場合には解析が容易になる，という特性があります．本研究室では，このような理論の相構造特に閉じ込めについての相構造を調べ，現実の強い力を記述するゲージ理論（QCD）とどのように繋がるかを格子数値計算などを用いて調べています．また，近年は量子異常マッチングと呼ばれる手法を用いた相構造の解析手法が注目を集めており，その手法に基づくQCD型理論や2次元シグマ模型の相構造研究を進めています．

関係する主な業績：
T.Fujimori, E.Itou, T.Misumi, M.Nitta, N.Sakai, JHEP08(2020)011
T.Misumi, Y.Tanizaki, M.Unsal, JHEP07(2019)018
M.Hongo, T.Misumi, Y.Tanizaki, JHEP02(2019)070
Y.Tanizaki, T.Misumi, N.Sakai, JHEP12(2017)056
T.Iritani, E.Itou, T.Misumi, JHEP11(2015)159
T.Misumi, T.Kanazawa, JHEP06(2014)181
三角樹弘,「量子異常の拡がり:素粒子論から物性論まで」数理科学 2020年1月号

左図：コンパクト化時空Adjoint QCDの相構造．中央図：Z3-QCDの数値計算結果．右図：ツイストCP2模型のポリャコフループ分布

3. 新しい格子離散化法やQCD型模型の格子シミュレーション


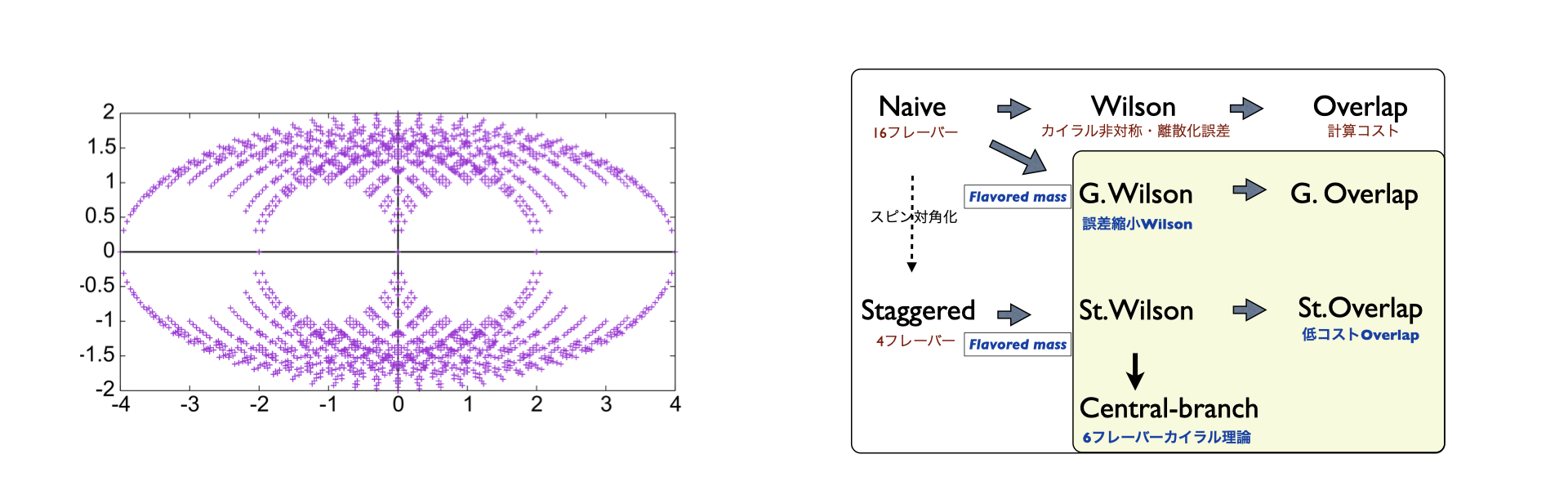
摂動論を超える場の量子論解析法の一般的枠組みの1つとして格子ゲージ理論があります．この理論では時空間を離散化し，格子点やそれらを繋ぐ線上に自由度を定義します．解析計算はこの場合も難しいですが，モンテカルロ法と呼ばれる統計的手法を用いた数値計算が有効であり，多くの成果を上げています．一方，離散化の結果として重大な問題が生じることや，現実の素粒子理論の解析が困難なこともあります．本研究室ではこの問題点を解消し得る格子模型を提案し，それに基づく数値計算の可能性を研究しています．

関係する主な業績：
J.Yumoto, T.Misumi, JHEP02(2022)104
T.Misumi, J.Yumoto, PRD102,034516(2020)
T.Misumi, JHEP12(2013)063
T.Misumi, JHEP08(2012)068
T.Misumi, T.Z.Nakano, T.Kimura, A.Ohnishi, PRD86,034501(2012)
M.Creutz, T.Kimura, T.Misumi, PRD83,094506(2011)
M.Creutz, T.Misumi, PRD82,074502(2010)

左図：Central-branch fermionのディラック固有値分布．右図：格子フェルミオンの相関図

4. 離散化された時空における超対称ゲージ理論の厳密解と数値計算


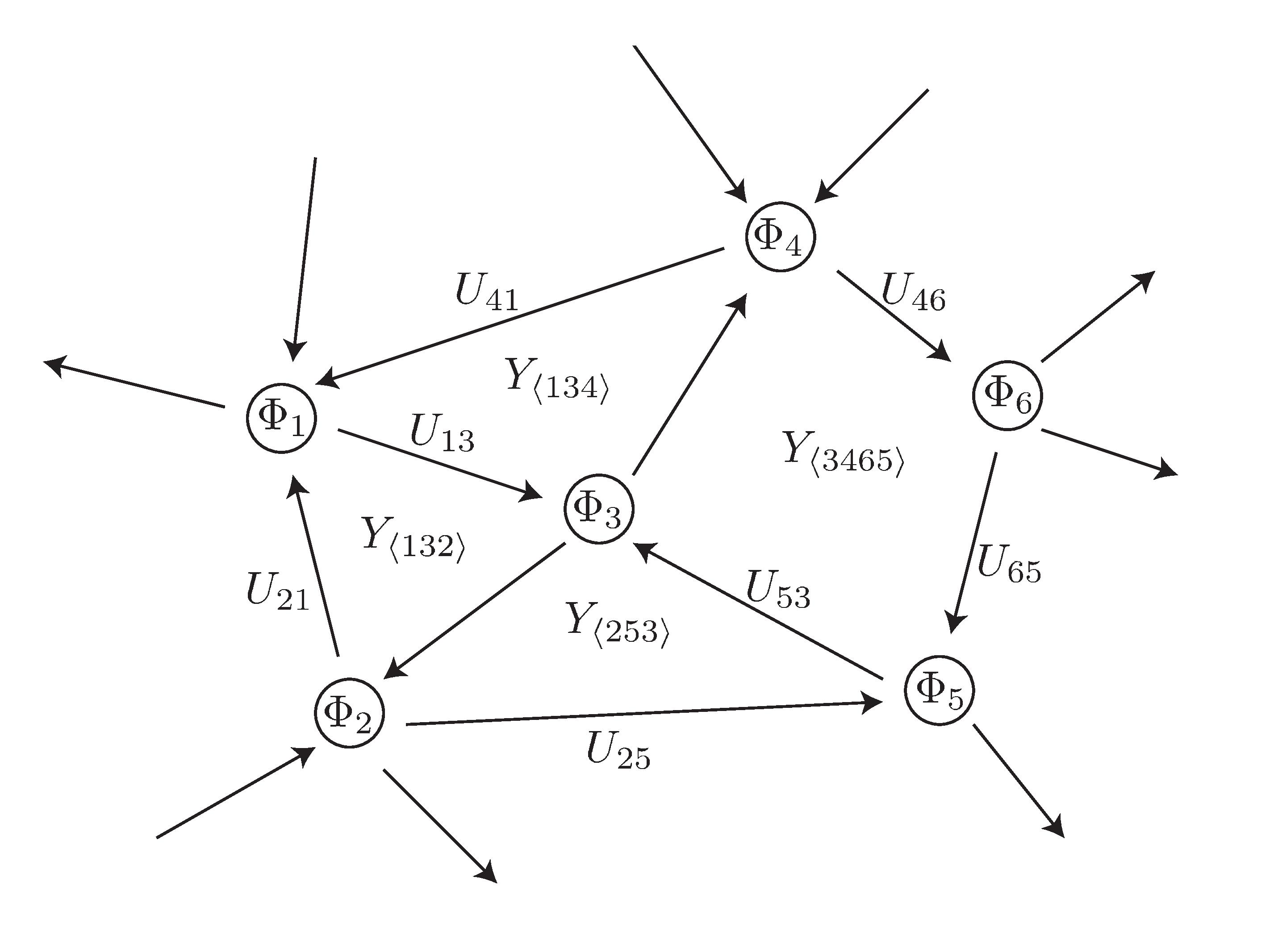
超対称ゲージ理論は高い対称性を持つため性質が良く，ある種の物理量については厳密に解ける場合もあります．本研究室では一般の離散化時空における超対称ゲージ理論について厳密解の導出と数値計算を行うことで，曲がった時空における超対称理論の性質を調べています．

関係する主な業績：
S.Kamata, S.Matsuura, T.Misumi, K.Ohta, PTEP(2016)123B01
S.Matsuura, T.Misumi, K.Ohta, PTEP(2015)033B07
S.Matsuura, T.Misumi, K.Ohta, PTEP(2014)123B01

離散化された時空における超対称ゲージ理論の自由度の例

5. 場の理論的観点に基づく物性模型の研究


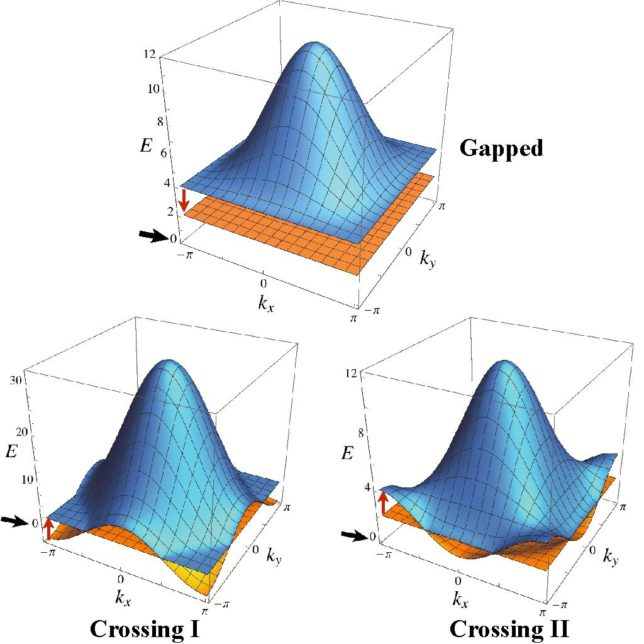
物性系は場の量子論で記述される身近な例であり，物性理論は上記のような研究成果を活かすことができる分野です．中でも近年注目を集めるようになったグラフィン系やトポロジカル絶縁体と言われる物質は，場の量子論の知識を用いることで理解が大いに進みました．本研究室では，ハニカム格子模型や平坦バンド模型と呼ばれる物性模型に注目し，模型の一般化，トポロジカルな性質の研究，電磁応答の解析などを行っています．

関係する主な業績：
T.Misumi, H.Aoki, PRB96,155137(2017)
T.Kimura, T.Misumi, PTP123,63(2010)
T.Misumi, K.Shizuya, PRB77,195423(2008)

平坦バンド構造の一例

6. ホログラフィック模型に基づく場の量子論の非摂動的解析


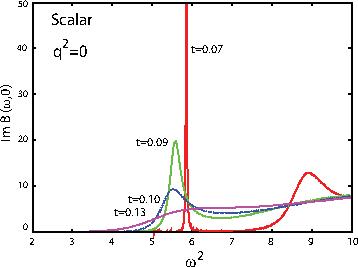
場の量子論の非摂動的側面を理解する方法として，ゲージ重力対応を用いる手法があります．超弦理論を考えると，ある種のゲージ場の量子論と重力理論が等価性を持つことが予想され，その予想に基づいて構成されたゲージ理論に対応する重力模型をホログラフィック模型と呼びます．本研究室では，このような模型を用いた有限温度QCD系の解析を行っています．

関係する主な業績：
M.Fujita, K.Fukushima, T.Kikuchi, T.Misumi, M.Murata, PRD81,065024(2010)
M.Fujita, K.Fukushima, T.Misumi, M.Murata, PRD80,035001(2009)

ホログラフィック模型により計算した高温での中間子溶解の様子

修士論文・卒業論文研究テーマ


博士論文研究テーマ：
　2023年度
　「Lattice fermions based on graph theory and topology(湯本)」

修士論文研究テーマ：
　2022年度
　「場の量子論における真空のエネルギーと宇宙加速膨張の現象論的考察(千頭和)」
　「高次元におけるポアンカレ群の表現と一般スピン粒子の分類(津金澤)」
　2021年度
　「基本表現と随伴表現フェルミオンを含むコンパクト時空上のQCDの閉じ込め相転移(湯川)」
　2020年度
　「位相幾何学的手法に基づく格子上のカイラルゲージ理論と大統一理論の構成(湯本)」
　2019年度
　「一般の場の量子論と重力理論についてのゲージ/重力対応(小原)」
　「場の量子論における真空エネルギーとカシミール効果の解析法(塚本)」
　2018年度
　「高次摂動計算に基づく量子トンネル効果の解析(高畑)」

卒業論文研究テーマ：
　2023年度
　「量子暗号の原理と量子誤り訂正(竹村)」
　「格子上のスカラー場理論とゲージ理論(下池)」
　「シュレディンガー・ニュートン方程式を用いた重力場の量子力学的理解(東浦)」
　「ニュートリノ振動の原理と実験に基づく質量推定について(享保)」
　「Physics-Informed Neural Network(PINN) を用いた量子系の時間発展にについて(濱田)」
　「機械学習を用いた量子 Heisenberg 模型の基底状態の導出について(石原)」
　2022年度
　「波動関数の自己重力を考慮したシュレーディンガー方程式(工藤)」
　「量子論におけるベルの不等式の破れとその限界について(西川)」
　「エントロピー増大則の微視的導出 -シュレディンガー方程式の時間反転対称性との矛盾-(田中)」
　「連成振動系の量子力学 -場の量子論の出現-(森本)」
　「量子暗号と光の場の量子論(中野)」
　「量子テレポーテーションの原理と実用化の可能性(武田)」
　2020年度
　「量子テレポーテーション(崔)」
　「一般相対性理論とブラックホール解(千頭和)」
　「物理学におけるリー代数(津金澤)」
　2019年度
　「均一磁場中スピン1/2系の量子論的歳差運動(小笠原)」
　「特殊相対論の基礎(柳田)」
　「マクスウェル方程式の相対論的定式化(湯川)」
　2018年度
　「素粒子物理学におけるリー群(湯本)」
　「量子情報通信における非局所性とベルの不等式(奥山)」
　2017年度
　「量子力学の非局所性とベルの不等式(逢坂)」
　「一般相対性理論と重力波の検出原理(小原)」
　2016年度
　「経路積分法と摂動計算に基づく量子系の解析(李)」