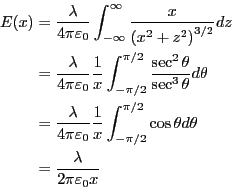問題2.2.2

無限に長い直線上に単位長さ当たり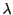$\lambda$の電荷が分布している。 この電荷がx軸上に作る電場を計算せよ。

===== 解答 =====

幾何学的な対称性より、z軸方向の電場は存在しない。また、系は軸対称 なので、接線方向の電場も存在しない。従って、動径方向の電場のみを 考えれば良い。z軸に沿って電荷が分布していると考えて計算を行う。

z軸上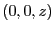$(0,0,z)$に存在する電荷が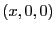$(x,0,0)$に作る電場の大きさは

$$\begin{eqnarray*} dE(z) &=& \frac{\lambda dz}{4\pi\varepsilon_0} \frac{1}{x^2+z^2} \end{eqnarray*}$$

この位置における動径方向はx軸方向である。その方向の成分は

$$\begin{eqnarray*} dE_\bot(z) &=& \frac{\lambda dz}{4\pi\varepsilon_0} \frac{1}{x^2+z^2} \frac{x}{\sqrt{x^2+z^2}} \end{eqnarray*}$$

求めるべき電場の大きさは

$$\begin{eqnarray*} E(x) &=& \frac{\lambda}{4\pi\varepsilon_0}\int_{-\infty}^\inft... ...\cos \theta d\theta \\ &=& \frac{\lambda}{2\pi\varepsilon_0 x} \end{eqnarray*}$$

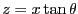ただし、 $z = x \tan \theta$を用いて、変数変換を行っている。