



: 問題3.5.4
: 変動する電磁場と物質
: 誘電体中の電磁波
目次
誘電体中では、光速は周波数に応じて変化しても電磁波のエネルギーは誘電体に
よって吸収されないとして、電磁波の伝搬を取り扱った。導体中では、誘電体
中と異なって、電磁波のエネルギーの導体による吸収が無視できな
くなる。言い換えると、導体中を進む電磁波の振幅はだんだん減少する。
導体中の電磁波を考える場合、電流の効果を考慮しないといけない。その点が真
空中と異なっている。
電荷はないが(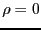 )、電流はある導体中を伝わる波を考える。
また、
)、電流はある導体中を伝わる波を考える。
また、
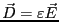 、そして
、そして
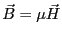 としている。
よって、マクスウェルの方程式は
電界
としている。
よって、マクスウェルの方程式は
電界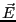 と磁場
と磁場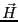 だけで表せ、
だけで表せ、
となる。ここで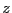 方向に伝わる平面波を考えると、すべての量は
方向に伝わる平面波を考えると、すべての量は
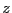 と
と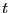 だけの関数であるから、マクスウェルの方程式は
だけの関数であるから、マクスウェルの方程式は
となる。ただし、
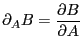 と略記
している。
と略記
している。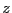 方向に進む平面波を考えているので、
方向に進む平面波を考えているので、
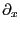 や
や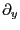 を作用させると結果は必ずゼロになる。
したがって、
を作用させると結果は必ずゼロになる。
したがって、
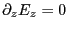 が結論づけられる。しかも今は
が結論づけられる。しかも今は
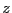 方向に進む波を考えているので、
方向に進む波を考えているので、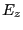 は定数でなければ
ならないことが分かる。ここでは以後の計算を簡単にするためにゼロとする。
同様にして
は定数でなければ
ならないことが分かる。ここでは以後の計算を簡単にするためにゼロとする。
同様にして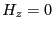 が結論できるので、電磁波は
「横波」であることがわかる。
が結論できるので、電磁波は
「横波」であることがわかる。
波動を表す式は
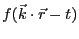 のように表されることに
注意。今の場合は,
のように表されることに
注意。今の場合は,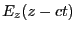 となる。
となる。
ここで、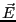 の方向を
の方向を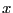 方向にとると、定義より
方向にとると、定義より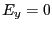 である。
電流
である。
電流
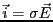 である。ただし、
である。ただし、
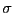 は周波数依存性がないとし
て静電界の値を使うことにする。電界は
は周波数依存性がないとし
て静電界の値を使うことにする。電界は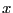 方向にしか値を持たないので、
方向にしか値を持たないので、
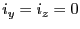 が結論づけられる。
が結論づけられる。
次に、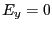 と上記の方程式を合わせて、
と上記の方程式を合わせて、
が得られる。すなわち、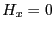 となり
となり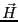 は
は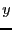 成分だけを持つ。
成分だけを持つ。
結局、マクスウェルの方程式は以下のにように簡略できる。
最初の2式は横波であることを示し、第3,4式は波に伴う電界と磁場の変動方向が
直交していることを表している。
最後の2つの方程式より、
整理すると、
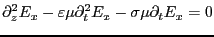 |
|
|
(3.61) |
となる。ここで、振動する電磁場を複素数で次のように表して,
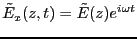 |
|
|
(3.62) |
微分方程式を解くことにする。元の微分方程式は、
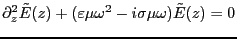 |
|
|
(3.63) |
となる。
もしも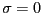 ならば、
ならば、
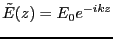 |
|
|
(3.64) |
が解になる。ただし、
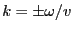 、
、
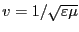 であ
る。これを用いると、
であ
る。これを用いると、
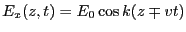 |
|
|
(3.65) |
となり、空間的に進む波を表していることがわかる。
導体中なので、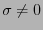 であるので、複素数の
であるので、複素数の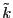 を許して
を許して
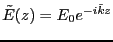 とおいて解を求めると、
とおいて解を求めると、
![$\displaystyle [-\tilde{k}^2 + (\varepsilon \mu \omega^2 - i \sigma \mu \omega)]
E_0 = 0$](img1563.png) |
|
|
(3.66) |
となる。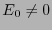 でないと意味がないので、係数がゼロでないといけない。
従って、
でないと意味がないので、係数がゼロでないといけない。
従って、
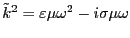 |
|
|
(3.67) |
右辺の第1項と第2項の大きさを比較しよう。
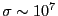 [
[
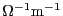 ]で、
]で、
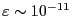 [Fm
[Fm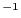 ]であるから、
]であるから、
![$\displaystyle \frac{\sigma}{\varepsilon} \sim 10^{18} [{\rm s}^{-1}]$](img1569.png) |
|
|
(3.68) |
である。このようにして、
可視光(
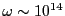 )を考えたとしても第1項は第
2項と比較して無視できることがわかった。従って、
)を考えたとしても第1項は第
2項と比較して無視できることがわかった。従って、
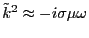 |
|
|
(3.69) |
あるいは、
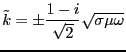 |
|
|
(3.70) |
が得られる。結局、
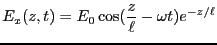 |
|
|
(3.71) |
ただし、
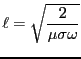 |
|
|
(3.72) |
となる。この式は、導体中で進まず減衰する「波」を表している。
マイクロ波(
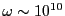 )の場合、
)の場合、
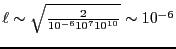 [m]になる。
マイクロ波の波長はcm程度あるから、電磁波は導体中には全くと言って良いほど
侵入できないことがわかる。
[m]になる。
マイクロ波の波長はcm程度あるから、電磁波は導体中には全くと言って良いほど
侵入できないことがわかる。




: 問題3.5.4
: 変動する電磁場と物質
: 誘電体中の電磁波
目次
Administrator
平成25年7月6日
![]() )、電流はある導体中を伝わる波を考える。
また、
)、電流はある導体中を伝わる波を考える。
また、
![]() 、そして
、そして
![]() としている。
よって、マクスウェルの方程式は
電界
としている。
よって、マクスウェルの方程式は
電界![]() と磁場
と磁場![]() だけで表せ、
だけで表せ、
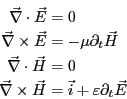
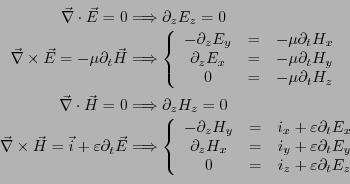
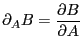 と略記
している。
と略記
している。のように表されることに 注意。今の場合は,
となる。
![]() の方向を
の方向を![]() 方向にとると、定義より
方向にとると、定義より![]() である。
電流
である。
電流
![]() である。ただし、
である。ただし、
![]() は周波数依存性がないとし
て静電界の値を使うことにする。電界は
は周波数依存性がないとし
て静電界の値を使うことにする。電界は![]() 方向にしか値を持たないので、
方向にしか値を持たないので、
![]() が結論づけられる。
が結論づけられる。
![]() と上記の方程式を合わせて、
と上記の方程式を合わせて、
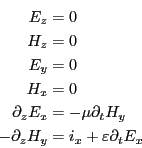
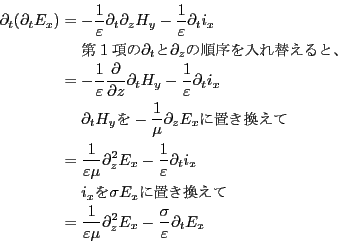
![]() ならば、
ならば、
![]() であるので、複素数の
であるので、複素数の![]() を許して
を許して
![]() とおいて解を求めると、
とおいて解を求めると、
![]() )の場合、
)の場合、
![]() [m]になる。
マイクロ波の波長はcm程度あるから、電磁波は導体中には全くと言って良いほど
侵入できないことがわかる。
[m]になる。
マイクロ波の波長はcm程度あるから、電磁波は導体中には全くと言って良いほど
侵入できないことがわかる。