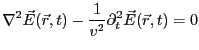 |
(3.58) |
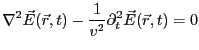 |
(3.58) |
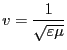 |
(3.59) |
| (3.60) |
物質1,2がありそれぞれの絶対屈折率を![]() とするとき、
とするとき、![]() を物質2
の1に対する相対屈折率という。
を物質2
の1に対する相対屈折率という。
真空中ではすべての周波数の電磁波の速度は光速で一定であった。従って、任意 の波形の波、すなわち異なった周波数の波の重ねあわせ、が真空中を伝搬すると き、その形は変化しない。ところが、物質中では周波数に応じてその電磁波の早 さは異なる。図 3.19参照。ここでは、分散がある場合とない場合 の波(波束)の伝搬の例を図示している。具体的な波を表す式は、
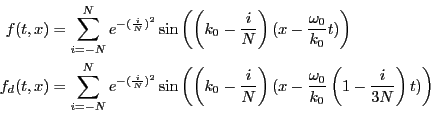
![\includegraphics[width=5cm]{wave_packet.eps}](img1539.png)
|
従って、波の形が変化する場合がある。このような現象のことを 波の分散という。虹も波の分散現象の現れである。