



: 誘電体中の電磁波
: エネルギーの散逸
: 問題3.5.2
目次
静電界の比誘電率が4.5の物質で、その中の電子の固有振動数が
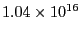 s
s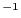 の誘電体がある。振動数
の誘電体がある。振動数
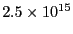 s
s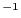 (赤い光)と
(赤い光)と
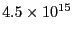 s
s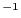 (青い)の
光に対する比誘電率を求めよ。ただし、緩和時間は十分に長く誘電率の虚数部分
は無視できると仮定する。
(青い)の
光に対する比誘電率を求めよ。ただし、緩和時間は十分に長く誘電率の虚数部分
は無視できると仮定する。
===== 解答 =====
虚数部分を無視すると、
である。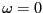 のとき、
のとき、
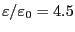 を用いると、
を用いると、
となる。
赤い光の場合
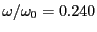 、
青い光の場合
、
青い光の場合
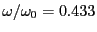 であるから、そのときの比誘電率は
それぞれ、4.71と5.31になる。
であるから、そのときの比誘電率は
それぞれ、4.71と5.31になる。
Administrator
平成25年7月6日
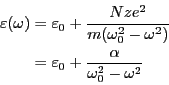
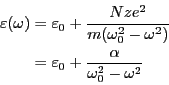
![]() 、
青い光の場合
、
青い光の場合
![]() であるから、そのときの比誘電率は
それぞれ、4.71と5.31になる。
であるから、そのときの比誘電率は
それぞれ、4.71と5.31になる。