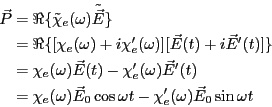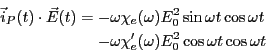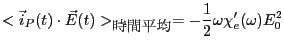: 問題3.5.1
: 変動する電磁場と物質
: 抵抗がある場合
目次
誘電体中の電界の持つエネルギーは
となってしまう。この虚数のエネルギーの意味を考えてみよう。
物理的に意味のある分極ベクトル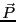 は複素数で表した分極ベクトル
は複素数で表した分極ベクトル
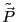 の実数部である。
の実数部である。
分極電流は分極の時間微分で与えられるから、
となる。この分極電流は電界中を動いているわけだから、単位時間、単位体積当
たり
のエネルギーを散逸する。第1項は時間平均を取るとゼロになる。第2項は時間平
均をとると、
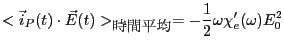 |
|
|
(3.57) |
となる。先のモデルに従えば、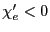 なので、
電界のエネルギーが散逸されることが分かる。
ミクロに見れば、電界によって電子が動く。その動きに対して抵抗力が働いて、
エネルギーを散逸していることを意味している。
なので、
電界のエネルギーが散逸されることが分かる。
ミクロに見れば、電界によって電子が動く。その動きに対して抵抗力が働いて、
エネルギーを散逸していることを意味している。
最初の虚数のエネルギーは電界のエネルギーの散逸が起こることを意味している。
Administrator
平成25年7月6日
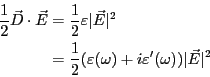
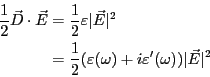
![]() は複素数で表した分極ベクトル
は複素数で表した分極ベクトル
![]() の実数部である。
の実数部である。