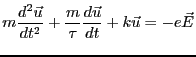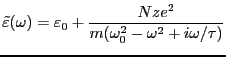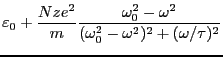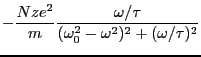: エネルギーの散逸
: 誘電体中の振動電界
: 誘電体中の振動電界
目次
電子の運動に速度に比例した抵抗がある場合を考える。電子の運動方程式は、
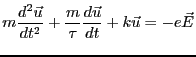 |
|
|
(3.51) |
になる。ここで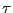 は緩和時間で、電界が急に変化した場合この程度の時間が
たてば電子はその電界の変化に追随する。
抵抗がない場合と同様に複素数を用いて、微分方程式を解くと、
は緩和時間で、電界が急に変化した場合この程度の時間が
たてば電子はその電界の変化に追随する。
抵抗がない場合と同様に複素数を用いて、微分方程式を解くと、
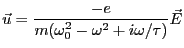 |
|
|
(3.52) |
となる。誘電率は複素数になり、
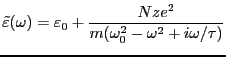 |
|
|
(3.53) |
となる。誘電率を実数部と虚数部に分けると、
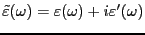 |
|
|
(3.54) |
ただし、
である。
図 3.18:
誘電率の周波数依存性(抵抗のある場合)
|
|
Administrator
平成25年7月6日